Relations and Functions
NCERT Textbook Solution (Laptop/Desktop is best to view this page)
NCERT Solutions for Class 11 Maths Chapter 2
Relations and Functions Class 11
Chapter 2 Relations and Functions Exercise 2.1, 2.2, 2.3, miscellaneous Solutions
Exercise 2.1 : Solutions of Questions on Page Number : 33
Q1 :
If ![]() , find the values of xand y.
, find the values of xand y.
Answer :
It is given
that ![]() .
.
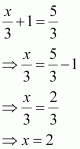 Since the ordered pairs are equal, the corresponding
elements will also be equal. Therefore,
Since the ordered pairs are equal, the corresponding
elements will also be equal. Therefore, ![]() and
and ![]() .
.
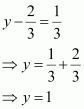 |
∴ x= 2 and y= 1
![]()
Q2 :
If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A x B)?
Answer :
It is given that set A has 3 elements and the elements of set B are 3, 4, and 5.
⇒ Number of elements in set B = 3 Number of elements in (A x B)
= (Number of elements in A) x (Number of elements in B)
= 3 x 3 = 9
Thus, the number of elements in (A x B) is 9.
![]()
Q3 :
If G = {7, 8} and H = {5, 4, 2}, find G x H and H x G.
Answer :
G = {7, 8} and H = {5, 4, 2}
We know that the Cartesian product P x Q of two non-empty sets P and Q is defined as P x Q = {(p, q): p∈P, q ∈Q}
∴G x H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
H x G = {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}
Q4 :
State whether each of the following statement are true or false. If the statement is false, rewrite the given statement correctly.
(i) If P = {m, n} and Q = {n, m}, then P x Q = {(m, n), (n, m)}.
(ii) If A and B are non-empty sets, then A x B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
(iii) If A = {1, 2}, B = {3, 4}, then A x (B ∩ Φ) = Φ.
Answer :
(i) False
If P = {m, n} and Q = {n, m}, then
P x Q = {(m, m), (m, n), (n, m), (n, n)}
(ii) True
(iii)
True
Q5 :
If A = {-1, 1}, find A x A x A.
Answer :
It is known that for any non-empty set A, A x A x A is defined as A x A x A = {(a, b, c): a, b, c ∈ A}
It is given that A = {-1, 1}
∴ A x A x A = {(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1),
(1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)}
Q6 :
If A x B = {(a, x), (a, y), (b, x), (b, y)}. Find A and B.
Answer :
It is given that A x B = {(a, x), (a, y), (b, x), (b, y)}
We know that the Cartesian product of two non-empty sets P and Q is defined as P x Q = {(p, q): p ∈P, q ∈Q}
![]() ∴ A is the set of all first elements and B is the set of all second
elements. Thus, A = {a, b} and B = {x, y}
∴ A is the set of all first elements and B is the set of all second
elements. Thus, A = {a, b} and B = {x, y}
Q7 :
Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that
(i) A x (B ∩C) = (A x B) ∩(A x C)
(ii) A x C is a subset of B x D
Answer :
(i) To verify: A x (B ∩C) = (A x B) ∩(A x C) We have B ∩C = {1, 2, 3, 4} ∩{5, 6} = Φ
∴L.H.S. = A x (B ∩C) = A x Φ = Φ
A x B = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
A x C = {(1, 5), (1, 6), (2, 5), (2, 6)}
∴ R.H.S. = (A x B) ∩(A x C) = Φ
∴L.H.S. = R.H.S
Hence, A x (B ∩C) = (A x B) ∩(A x C)
(ii) To verify: A x C is a subset of B x D A x C = {(1, 5), (1, 6), (2, 5), (2, 6)}
B x D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
![]() We can observe that all
the elements of set A x C are
the elements of set B x D. Therefore, A x C is a subset of B x D.
We can observe that all
the elements of set A x C are
the elements of set B x D. Therefore, A x C is a subset of B x D.
Q8 :
Let A = {1, 2} and B = {3, 4}. Write A x B. How many subsets will A x B have? List them.
Answer :
A = {1, 2} and B = {3, 4}
∴A x B = {(1, 3), (1, 4), (2, 3), (2, 4)}
⇒ n(A x B) = 4
We know that if C is a set with n(C) = m, then n[P(C)] = 2m. Therefore, the set A x B has 24= 16 subsets. These are
Φ, {(1, 3)}, {(1, 4)}, {(2, 3)}, {(2, 4)}, {(1, 3), (1, 4)}, {(1, 3), (2, 3)},
{(1, 3), (2, 4)}, {(1, 4), (2, 3)}, {(1, 4), (2, 4)}, {(2, 3), (2, 4)},
{(1, 3), (1, 4), (2, 3)}, {(1, 3), (1, 4), (2, 4)}, {(1, 3), (2, 3), (2, 4)},
{(1, 4), (2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3), (2, 4)}
Q9 :
Let A and B be two sets such that n(A) = 3 and n (B) = 2. If (x, 1), (y, 2), (z, 1) are in A x B, find A and B, wherex, y and z are distinct elements.
Answer :
It is given that n(A) = 3 and n(B) = 2; and (x, 1), (y, 2), (z, 1) are in A x B. We know that A = Set of first elements of the ordered pair elements of A x B B = Set of second elements of the ordered pair elements of A x B.
![]() ∴ x, y, and zare the elements of A; and 1
and 2 are the elements of B. Since n(A) = 3 and
n(B) = 2, it is clear that A = {x, y, z} and B = {1,
2}.
∴ x, y, and zare the elements of A; and 1
and 2 are the elements of B. Since n(A) = 3 and
n(B) = 2, it is clear that A = {x, y, z} and B = {1,
2}.
Q10 :
The Cartesian product A x A has 9 elements among which are found (-1, 0) and (0, 1). Find the set A and the remaining elements of A x A.
Answer :
We know that if n(A) = p and n(B) = q, then n(A x B) = pq.
∴ n(A x A) = n(A) x n(A)
It is given that n(A x A) = 9
∴ n(A) x n(A) = 9
⇒ n(A) = 3
The ordered pairs (-1, 0) and (0, 1) are two of the nine elements of A x A.
We know that A x A = {(a, a): a ∈A}. Therefore, -1, 0, and 1 are elements of A. Since n(A) = 3, it is clear that A = {-1, 0, 1}.
The remaining elements of set A x A are (-1, -1), (-1, 1), (0, -1), (0, 0),
(1, -1), (1, 0), and (1, 1)
Exercise 2.2 : Solutions of Questions on Page Number : 35
Q1 :
Let A = {1, 2, 3, ... , 14}. Define a relation R from A to A by R = {(x, y): 3x - y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
Answer :
The relation R from A to A is given as R = {(x, y): 3x - y = 0, where x, y ∈ A}
i.e., R = {(x, y): 3x = y, where x, y ∈ A}
∴R = {(1, 3), (2, 6), (3, 9), (4, 12)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
∴Domain of R = {1, 2, 3, 4}
The whole set A is the codomainof the relation R.
∴Codomain of R = A = {1, 2, 3, ..., 14}
The range of R is the set of all second elements of the ordered pairs in the relation.
∴Range of R = {3, 6, 9, 12}
Q2 :
Define a relation R on the set Nof natural numbers by R = {(x, y): y= x+ 5, xis a natural number less than 4; x,y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
Answer :
R = {(x, y): y= x+ 5, xis a natural number less than 4, x, y ∈ N} The natural numbers less than 4 are 1, 2, and 3.
∴R = {(1, 6), (2, 7), (3, 8)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
∴ Domain of R = {1, 2, 3}
The range of R is the set of all second elements of the ordered pairs in the relation.
∴ Range of R = {6, 7, 8}
Q3 :
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between xand yis odd; x ∈A, y ∈B}. Write R in roster form.
Answer :
A = {1, 2, 3, 5} and B = {4, 6, 9}
R = {(x, y): the difference between xand yis odd; x ∈A, y ∈B}
∴R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}
Q4 :
The given figure shows a relationship between the sets P and Q. write this relation
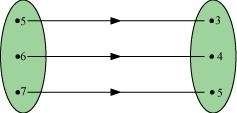 (i) in set-builder form (ii) in roster form.
What is its domain and range?
(i) in set-builder form (ii) in roster form.
What is its domain and range?
Answer :
According to the given figure, P = {5, 6, 7}, Q = {3, 4, 5}
(i) R = {(x, y): y = x- 2; x ∈P} or R = {(x, y): y = x- 2 for x= 5, 6, 7}
(ii) R = {(5, 3), (6, 4), (7, 5)}
Domain of R = {5, 6, 7}
Range of R = {3, 4, 5}
Q5 :
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by
{(a, b): a, b ∈A, bis exactly divisible by a}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
Answer :
A = {1, 2, 3, 4, 6}, R = {(a, b): a, b ∈A, bis exactly divisible by a}
(i) R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}
(ii) Domain of R = {1, 2, 3, 4, 6}
(iii)
Range of R = {1, 2, 3, 4, 6}
Q6 :
Determine the domain and range of the relation R defined by R = {(x, x+ 5): x ∈{0, 1, 2, 3, 4, 5}}.
Answer :
R = {(x, x+ 5): x ∈{0, 1, 2, 3, 4, 5}}
∴ R = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
∴Domain of R = {0, 1, 2, 3, 4, 5}
Range of R = {5, 6, 7, 8, 9, 10}
Q7 :
Write the relation R = {(x, x3): x is a prime number less than 10} in roster form.
Answer :
R = {(x, x3): x is a prime number less than 10}
The prime numbers less than 10 are 2, 3, 5, and 7.
∴R = {(2, 8), (3, 27), (5, 125), (7, 343)}
Q8 :
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
Answer :
It is given that A = {x, y, z} and B = {1, 2}.
∴ A x B = {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}
Since n(A x B) = 6, the number of subsets of A x B is 26.
Therefore, the number of relations from A to B is 26.
Q9 :
Let R be the relation on Zdefined by R = {(a, b): a, b ∈ Z, a - bis an integer}. Find the domain and range of R.
Answer :
R = {(a, b): a, b ∈ Z, a - bis an integer}
It is known that the difference between any two integers is always an integer.
∴Domain of R = Z
Range of R = Z
Exercise 2.3 : Solutions of Questions on Page Number : 44
Q1 :
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) {(1, 3), (1, 5), (2, 5)}
Answer :
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
Since 2, 5, 8, 11, 14, and 17 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 5, 8, 11, 14, 17} and range = {1}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Since 2, 4, 6, 8, 10, 12, and 14 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 4, 6, 8, 10, 12, 14} and range = {1, 2, 3, 4, 5, 6, 7}
(iii) {(1, 3), (1, 5), (2, 5)}
Since the same first element i.e., 1 corresponds to two different images i.e., 3 and 5, this relation is not a function.
Q2 :
Find the domain and range of the following real function:
(i) f(x) = โ|x| (ii) 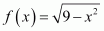 Answer :
Answer :
(i) f(x) = โ|x|, x ∈R
We know that |x| =
Since f(x) is defined for x ∈ R, the domain of fis R.
It can be observed that the range of f(x) = โ|x| is all real numbers except positive real numbers.
∴The range of fis (โ ![]() ,
0].
,
0].
(ii) ![]()
Since ![]() is defined for all real numbers that are greater than or
equal to โ3 and less than or equal to 3, the
domain of f(x) is {x : โ3 ≤ x ≤ 3} or [โ3, 3].
is defined for all real numbers that are greater than or
equal to โ3 and less than or equal to 3, the
domain of f(x) is {x : โ3 ≤ x ≤ 3} or [โ3, 3].
For any value of xsuch that โ3 ≤ x≤ 3, the value of f(x) will lie between 0 and 3.
∴The range of f(x) is {x: 0 ≤ x ≤ 3} or [0, 3].
Q3 :
A function fis defined by f(x) = 2x- 5. Write down the values of (i) f(0), (ii) f(7), (iii) f(-3)
Answer :
The given function is f(x) = 2x- 5. Therefore,
(i) f(0) = 2 x 0 - 5 = 0 - 5 = -5
(ii) f(7) = 2 x 7 - 5 = 14 - 5 = 9
(iii) f(-3) = 2 x (-3) - 5 = - 6 - 5 = -11
Q4 :
The function 't' which maps temperature in degree Celsius
into temperature in degree Fahrenheit is defined by ![]() .
.
Find (i) t(0) (ii) t(28) (iii) t(โ10) (iv) The value of C, when t(C) = 212
Answer :
The given function
is ![]() . Therefore,
. Therefore,
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv)
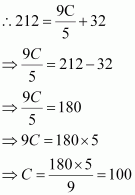 |
It is given that t(C) = 212
Thus, the value of t,when t(C) = 212, is 100.
![]()
Q5 :
Find the range of each of the following functions. (i) f(x) = 2 - 3x, x ∈ R, x> 0.
(ii) f(x) = x2+ 2, x, is a real number.
(iii) f(x) = x, xis a real number
Answer :
(i) f(x) = 2 โ 3x, x ∈ R, x> 0
The values of f(x) for various values of real numbers x> 0 can be written in the tabular form as
|
x |
0.01 |
0.1 |
0.9 |
1 |
2 |
2.5 |
4 |
5 |
|
|
f(x) |
1.97 |
1.7 |
โ0.7 |
โ1 |
โ4 |
โ5.5 |
โ10 |
โ13 |
|
Thus, it can be clearly observed
that the range of fis the set of all real
numbers less than 2. i.e.,
range of f= (โ ![]() , 2)
, 2)
Alter:
Let x > 0
⇒3x > 0
⇒ 2 โ3x< 2
⇒ f(x) < 2
∴Range of f = (โ ![]() , 2)
, 2)
(ii) f(x) = x2+ 2, x, is a real number
The values of f(x) for various values of real numbers xcan be written in the tabular form as
|
x |
0 |
ฑ0.3 |
ฑ0.8 |
ฑ1 |
ฑ2 |
ฑ3 |
|
|
|
f(x) |
2 |
2.09 |
2.64 |
3 |
6 |
11 |
|
.. |
Thus, it can be clearly observed
that the range of fis the set of all
real numbers greater than 2. i.e.,
range of f= [2, ![]() )
)
Alter:
Let x be any real number. Accordingly,
x2 ≥0
⇒ x2+ 2 ≥0 + 2
⇒ x2+ 2 ≥2
⇒ f(x) ≥2
∴ Range of f = [2, ![]() )
)
(iii) f(x) = x, x is a real number
It is clear that the range of fis the set of all real numbers.
∴ Range of f = R
Exercise Miscellaneous : Solutions of Questions on Page Number : 46
Q1 :
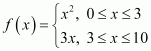 The relation
f is defined
by
The relation
f is defined
by
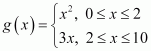 The relation gis defined by
The relation gis defined by
Show that f is a function and g is not a function.
Answer :
The relation fis defined
as 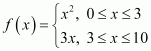 It is observed that for
It is observed that for
0 ≤ x < 3, f(x) = x2
3 < x ≤10, f(x) = 3x
Also, at x = 3, f(x) = 32 = 9 or f(x) = 3 ื 3 = 9 i.e., at x = 3, f(x) = 9
Therefore, for 0 ≤ x ≤10, the images of f(x) are unique. Thus, the given relation is a function.
The relation
gis defined as 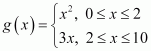
It can be observed that for x= 2, g(x) = 22 = 4 and g(x) = 3 ื 2 = 6
Hence, element 2 of the domain of the relation gcorresponds to two different images i.e., 4 and 6. Hence, this relation is not a function.
Q2 :
If f(x) = x2, find ![]() .
.
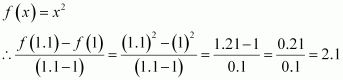 |
Answer :
![]()
Q3 :
Find the domain
of the function 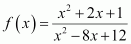 Answer :
Answer :
The given function is
It can be seen that function fis defined for all real numbers except at x= 6 and x= 2. Hence, the domain of fis R โ {2, 6}.
 Q4 :
Q4 :
Find the domain
and the range of the real function
fdefined by ![]() . Answer
:
. Answer
:
The given real function is ![]() .
.
It can be seen that ![]() is defined
for (xโ 1) ≥0.
i.e.,
is defined
for (xโ 1) ≥0.
i.e., ![]() is defined for x ≥1.
is defined for x ≥1.
Therefore, the domain of fis the set of all real numbers greater than or equal to 1
i.e., the domain of f= [1, ![]() ). As x ≥1 ⇒(x โ 1) ≥0 ⇒
). As x ≥1 ⇒(x โ 1) ≥0 ⇒ ![]()
Therefore, the range of fis the set of all real numbers greater than or equal to 0 i.e., the range of f= [0,
Q5 :
Find the domain and the range of the real function fdefined by f(x) = |x- 1|.
Answer :
The given real function isf(x) = |x- 1|.
It is clear that |x- 1| is defined for all real numbers.
∴Domain of f= R
Also, for x ∈ R, |x- 1| assumes all real numbers.
Hence, the range of fis the set of all non-negative real numbers.
Q6 :
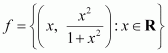 |
Let
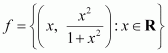 be
a function from Rinto R. Determine the range of f. Answer :
be
a function from Rinto R. Determine the range of f. Answer :
![]()
The range of fis the set of all second elements. It can be observed that all these elements are greater than or equal to 0 but less than 1.
![]() [Denominator is greater numerator] Thus, range of f= [0, 1)
[Denominator is greater numerator] Thus, range of f= [0, 1)
Q7 :
Let f, g: R รขโ R be defined,
respectively by f(x) = x + 1, g(x) =
2x โ 3. Find f+ g, fโ gand ![]() . Answer
:
. Answer
:
f, g: R รขโ R is defined as f(x) = x + 1, g(x) = 2x โ 3 (f+ g) (x) = f(x) + g(x) = (x + 1) + (2x โ 3) = 3x โ 2
∴(f + g) (x) = 3x โ 2
(f โ g) (x) = f(x) โ g(x) = (x + 1) โ (2xโ 3) = x+ 1 โ 2x+ 3 = โ x+ 4
∴ (f โ g) (x) = โx+ 4
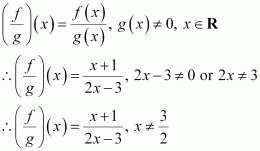
![]()
Q8 :
Let f = {(1, 1), (2, 3), (0, -1), (-1, -3)} be a function from Zto Zdefined by f(x) = ax+ b, for some integers a, b. Determine a, b.
Answer :
f = {(1, 1), (2, 3), (0, -1), (-1, -3)}
f(x) = ax+ b
(1, 1) ∈ f
⇒ f(1) = 1
⇒ a x 1 + b= 1
⇒ a+ b= 1 (0, -1) ∈ f
⇒ f(0) = -1
⇒ a x 0 + b= -1
⇒ b= -1
![]() On substituting b= -1 in a+ b= 1, we obtain a+ (-1) = 1
⇒ a= 1 + 1 = 2. Thus,
the respective values of aand bare 2 and -1.
On substituting b= -1 in a+ b= 1, we obtain a+ (-1) = 1
⇒ a= 1 + 1 = 2. Thus,
the respective values of aand bare 2 and -1.
Q9 :
Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b2}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R. Justify your answer in each case.
Answer :
R = {(a, b): a, b ∈ N and a = b2}
(i) It can be seen that 2 ∈ N;however, 2 ≠ 22 = 4.
Therefore, the statement (a, a) ∈ R, for all a ∈ N is not true.
(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 32. Now, 3 ≠ 92 = 81; therefore, (3, 9) ∠ฐ N
Therefore, the statement (a, b) ∈ R, implies (b, a) ∈ R is not true.
(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 42 and 4 = 22. Now, 16 ≠ 22 = 4; therefore, (16, 2) ∠ฐ N
Therefore, the statement (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R is not true.
Q10 :
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Are the following true?
(i) fis a relation from A to B (ii) fis a function from A to B. Justify your answer in each case.
Answer :
A = {1, 2, 3, 4} and B = {1, 5, 9, 11, 15, 16}
∴A x B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9),
(3, 11), (3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
It is given that f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
(i) A relation from a non-empty set A to a non-empty set B is a subset of the Cartesian product A x B. It is observed that fis a subset of A x B.
Thus, fis a relation from A to B.
(ii)
Since the same first element i.e., 2 corresponds to two different images i.e., 9 and 11, relation f is not a function.
Q11 :
Let fbe the subset of Z x Zdefined by f = {(ab, a+ b): a, b ∈ Z}. Is fa function from Zto Z: justify your answer.
Answer :
The relation fis defined as f = {(ab, a+ b): a, b ∈ Z}
We know that a relation ffrom a set A to a set B is said to be a function if every element of set A has unique images in set B.
Since 2, 6, -2, -6 ∈ Z, (2 x 6, 2 + 6), (-2 x -6, -2 + (-6)) ∈ f
i.e., (12, 8), (12, -8) ∈ f
It can be seen that the same first element i.e., 12 corresponds to two different images i.e., 8 and -8. Thus, relation fis not a function.
Q12 :
Let A = {9, 10, 11, 12, 13} and let f: A → Nbe defined by f(n) = the highest prime factor of n. Find the range off.
Answer :
A = {9, 10, 11, 12, 13}
f: A → Nis defined as
f(n) = The highest prime factor of n
Prime factor of 9 = 3
Prime factors of 10 = 2, 5
Prime factor of 11 = 11
Prime factors of 12 = 2, 3
Prime factor of 13 = 13
∴f(9) = The highest prime factor of 9 = 3 f(10) = The highest prime factor of 10 = 5 f(11) = The highest prime factor of 11 = 11 f(12) = The highest prime factor of 12 = 3 f(13) = The highest prime factor of 13 = 13
The range of fis the set of all f(n), where n ∈A.
∴Range of f= {3, 5, 11, 13}