Principle of Mathematical Induction
NCERT Textbook Solution (Laptop/Desktop is best to view this page)
NCERT Solutions for Class 11 Maths Chapter 4
Principle of Mathematical Induction Class 11
Chapter 4 Principle of Mathematical Induction Exercise 4.1 Solutions
Exercise 4.1 : Solutions of Questions on Page Number : 94
Q1 :
![]() Prove the following by using the principle of mathematical induction
for all n ∈ N:
Prove the following by using the principle of mathematical induction
for all n ∈ N:
Answer :
Let the given statement be P(n), i.e.,
P(n): 1 + 3 + 32
+ …+ 3n–1 = ![]()
For n = 1, we have
P(1):
1 =
![]() ,
which is true.
,
which is true.
Let P(k) be true for some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
1 + 3 + 32 + … + 3k–1 + 3(k+1) – 1
= (1 + 3 + 32 +… + 3k–1) + 3k
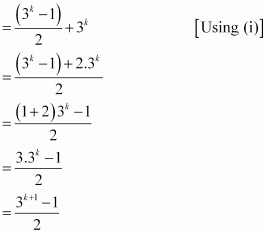 www.ncrtsolutions.in
www.ncrtsolutions.in
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q2 :
Prove the following by using the principle of mathematical
induction for all n ∈ N: 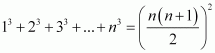
Answer :
Let the given statement be P(n), i.e.,
P(n):
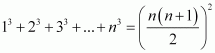
For n = 1, we have
P(1): 13
=
1 = 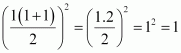 ,
which is true.
,
which is true.
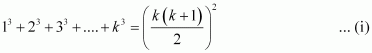 |
Let P(k) be true for some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
13 + 23 + 33 + … + k3 + (k + 1)3
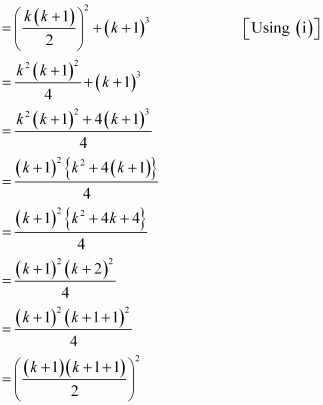 = (13 + 23 + 33 + …. + k3) + (k + 1)3
= (13 + 23 + 33 + …. + k3) + (k + 1)3
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q3 :
Prove the following by using the principle of mathematical induction for
all n ∈ N:  Answer :
Answer :
Let the given statement be P(n), i.e.,
P(n):
![]()
For n = 1, we have
P(1):
1 =
![]() which is true.
which is true.
Let P(k) be true for some positive integer k, i.e.,
![]()
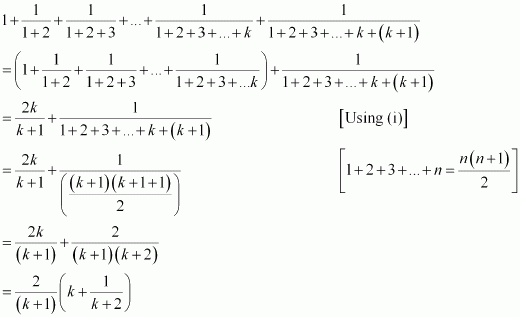 We shall now prove that P(k + 1) is true. Consider
We shall now prove that P(k + 1) is true. Consider
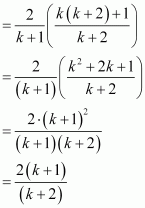 |
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q4 :
Prove the following
by using the principle of mathematical induction
for all n ∈ N: 1.2.3 + 2.3.4 + … + n(n + 1) (n
+ 2) = ![]()
Answer :
Let the given statement be P(n), i.e.,
P(n): 1.2.3 + 2.3.4 + … + n(n + 1) (n + 2) = ![]()
For n = 1, we have
P(1): 1.2.3 = 6
= ![]() , which is
true.
, which is
true.
Let P(k) be true for some positive integer k, i.e.,
1.2.3 + 2.3.4 + … + k(k + 1) (k + 2) ![]()
We shall now prove that P(k + 1) is true. Consider
1.2.3 + 2.3.4 + … + k(k + 1) (k + 2) + (k + 1) (k + 2) (k + 3)
= {1.2.3 + 2.3.4 + … + k(k + 1) (k + 2)} + (k + 1) (k + 2) (k + 3)
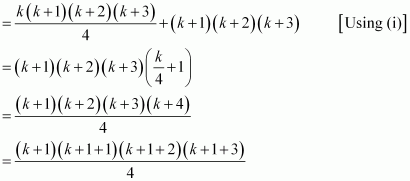 |
Thus, P(k + 1) is true whenever P(k) is
true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q5 :
Prove the following by using the principle of mathematical induction for all n ∈ N: ![]()
Answer :
Let the given statement be P(n), i.e.,
![]() P(n) :
P(n) :
For n = 1, we have
P(1):
1.3 = 3 ![]() ,
which is true.
,
which is true.
Let P(k) be true for some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
1.3 + 2.32 + 3.33 + … + k3k+ (k + 1) 3k+1
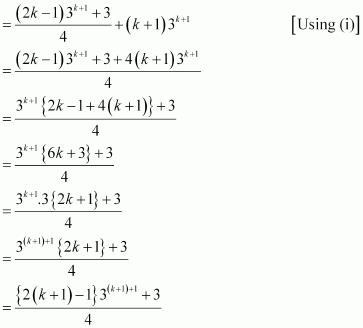 |
= (1.3 + 2.32 + 3.33 + …+ k.3k) + (k + 1) 3k+1
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q6 :
Prove the following by using the principle of mathematical induction for all n ∈ N: 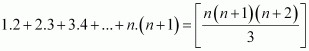
Answer :
Let the given statement be P(n), i.e.,
P(n):
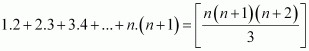
For n = 1, we have
P(1): ![]() , which is
true.
, which is
true.
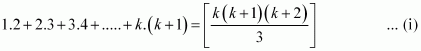 |
Let P(k) be true for some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
1.2 + 2.3 + 3.4 + … + k.(k + 1) + (k + 1).(k + 2)
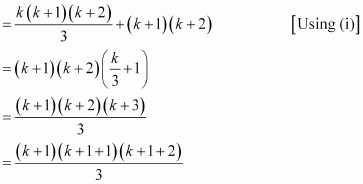 |
= [1.2 + 2.3 + 3.4 + … + k.(k + 1)] + (k + 1).(k + 2)
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q7 :
Prove the following by using the principle of mathematical induction for
all n ∈ N: 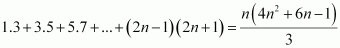 Answer :
Answer :
Let the given statement be P(n), i.e.,
![]() P(n):
P(n):
For n = 1, we have
![]() , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
We shall now prove that P(k + 1) is true.
Consider
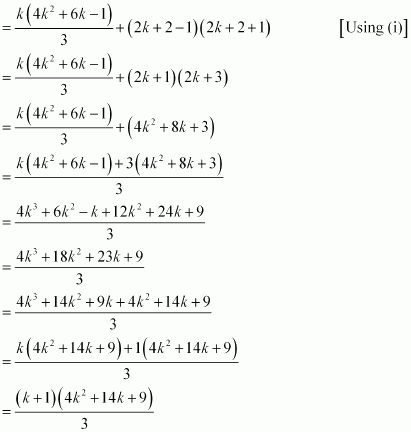 |
(1.3 + 3.5 + 5.7 + … + (2k – 1) (2k + 1) + {2(k + 1) – 1}{2(k + 1) + 1}
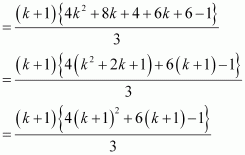
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q8 :
Prove the following by using the principle of mathematical induction for all n ∈ N: 1.2 + 2.22 + 3.22 + … + n.2n= (n - 1) 2n+1 + 2
Answer :
Let the given statement be P(n), i.e.,
P(n): 1.2 + 2.22 + 3.22 + … + n.2n = (n – 1) 2n+1 + 2
For n = 1, we have
P(1): 1.2 = 2 = (1 – 1) 21+1 + 2 = 0 + 2 = 2, which is true. Let P(k) be true for some positive integer k, i.e.,
1.2 + 2.22 + 3.22 + … + k.2k = (k – 1) 2k + 1 + 2 … (i)
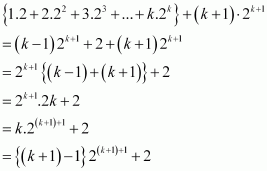 We shall now prove that P(k + 1) is true. Consider
We shall now prove that P(k + 1) is true. Consider
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q9 :
Prove the following by using the principle of mathematical
induction for all n ∈ N: ![]()
Answer :
Let the given statement be P(n), i.e.,
P(n):
![]()
For n = 1, we have
P(1): ![]() , which is
true.
, which is
true.
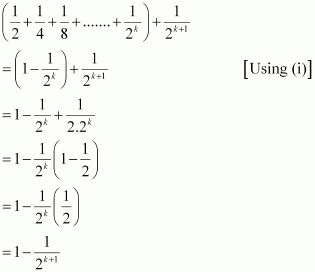 Let P(k) be true for
some positive integer k, i.e.,
Let P(k) be true for
some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q10 :
Prove the following by using the principle of mathematical induction for all n ∈ N: ![]()
Answer :
Let the given statement be P(n), i.e.,
P(n):
![]()
For n = 1, we have
We shall now prove that P(k + 1) is true. Consider
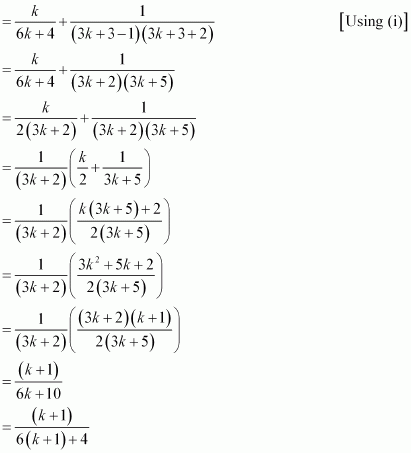 |
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q11 :
Prove the following by using the principle of mathematical induction for
all n ∈ N: 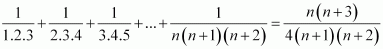 Answer :
Answer :
Let the given statement be P(n), i.e.,
P(n):
![]()
For n = 1, we have
![]() , which is true.
, which is true.
Let P(k) be true for some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
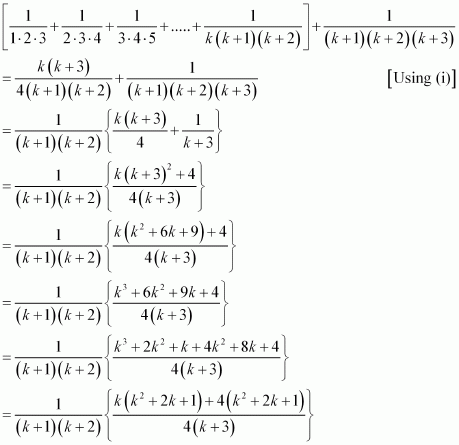
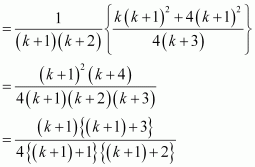
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q12 :
Prove the following by using the principle of mathematical induction for all n ∈ N: ![]()
Let the given statement be P(n), i.e.,
For n = 1, we have
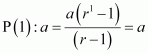 , which is true.
, which is true.
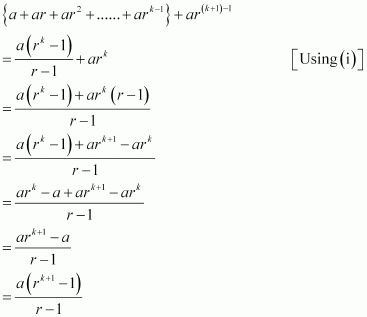 Let P(k) be true for
some positive integer k, i.e.,
Let P(k) be true for
some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q13 :
Prove the following by using the principle of mathematical induction for all n ∈ N: 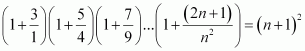
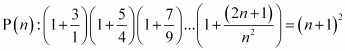 |
Let the given statement be P(n), i.e.,
For n = 1, we have
![]()
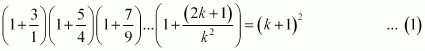 |
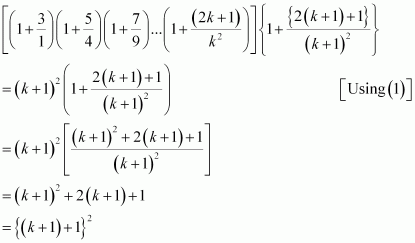 Let P(k) be true for
some positive integer k, i.e.,
Let P(k) be true for
some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q14 :
Prove the following by using the principle of mathematical
induction for all n ∈ N: ![]()
Answer :
Let the given statement be P(n), i.e.,
For n = 1, we have
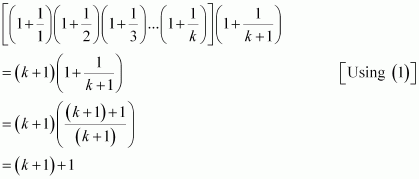
We shall now prove that P(k + 1) is true. Consider
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q15 :
Prove the following by using the principle of mathematical induction for all n ∈ N: ![]()
Answer :
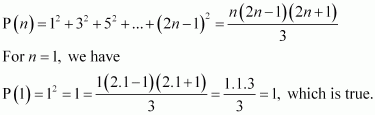 |
Let the given statement be P(n), i.e.,
Let P(k) be true for some positive integer k, i.e.,
![]()
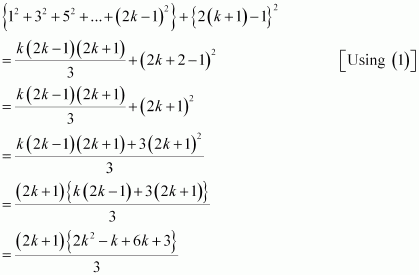 We shall now prove that P(k + 1) is true. Consider
We shall now prove that P(k + 1) is true. Consider
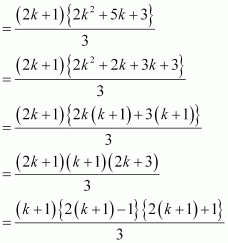 |
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q16 :
Prove the following by using the principle of mathematical induction for
all n ∈ N: 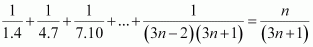 Answer :
Answer :
Let the given statement be P(n), i.e.,
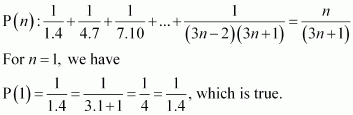
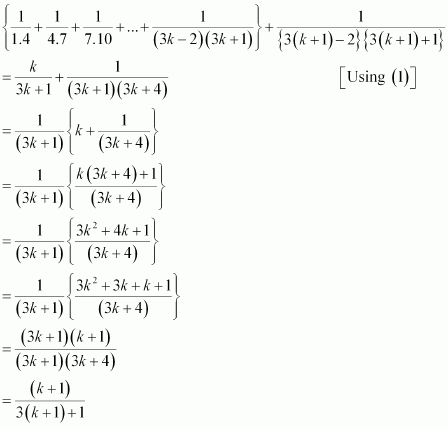 Let P(k) be true for
some positive integer k, i.e.,
Let P(k) be true for
some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q17 :
Prove the following by using the principle of mathematical induction for
all n ∈ N: 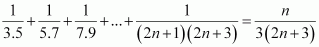 Answer :
Answer :
Let the given statement be P(n), i.e.,
For n = 1, we have
![]()
![]() , which is true. Let P(k) be true
for some positive integer k, i.e.,
, which is true. Let P(k) be true
for some positive integer k, i.e.,
We shall now prove that P(k + 1) is true. Consider
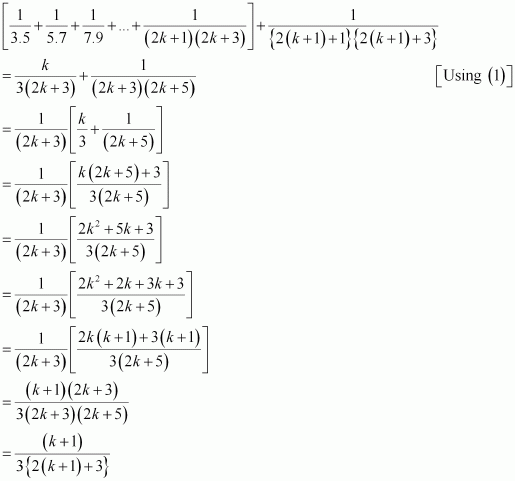
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q18 :
Prove the following by using the principle of mathematical induction for all n ∈ N: ![]()
Answer :
Let the given statement be P(n), i.e.,
It can be noted that P(n) is
true for n
= 1 since ![]() . Let P(k) be true
for some positive integer k, i.e.,
. Let P(k) be true
for some positive integer k, i.e.,
![]()
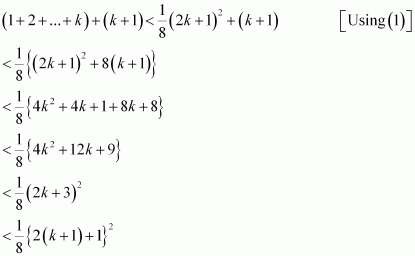 We shall now prove
that P(k + 1) is true whenever
P(k) is true.
Consider
We shall now prove
that P(k + 1) is true whenever
P(k) is true.
Consider
Hence, ![]() Thus, P(k + 1) is true whenever
P(k) is true.
Thus, P(k + 1) is true whenever
P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q19 :
Prove the following by using the principle of mathematical induction for all n ∈ N: n (n + 1) (n + 5) is a multiple of 3.
Answer :
Let the given statement be P(n), i.e.,
P(n): n (n + 1) (n + 5), which is a multiple of 3.
It can be noted that P(n) is true for n = 1 since 1 (1 + 1) (1 + 5) = 12, which is a multiple of 3. Let P(k) be true for some positive integer k, i.e.,
k (k + 1) (k + 5) is a multiple of 3.
∴k (k + 1) (k + 5) = 3m, where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true. Consider
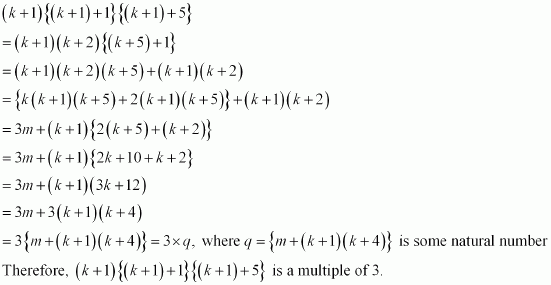
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q20 :
Prove the following by using the principle of mathematical induction for all n ∈ N: 102n - 1 + 1 is divisible by 11.
Answer :
Let the given statement be P(n), i.e., P(n): 102n – 1 + 1 is divisible by 11.
It can be observed that P(n) is true for n = 1 since P(1) = 102.1 – 1 + 1 = 11, which is divisible by 11. Let P(k) be true for some positive integer k, i.e.,
102k– 1 + 1 is divisible by 11.
∴102k– 1 + 1 = 11m, where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true. Consider
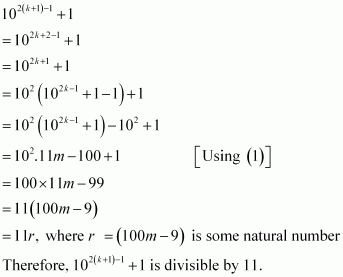
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q21 :
Prove the following by using the principle of mathematical induction for all n ∈ N: x2n - y2n is divisible by x+ y.
Answer :
Let the given statement be P(n), i.e., P(n): x2n – y2n is divisible by x + y.
It can be observed that P(n) is true for n = 1.
This is so because x2 ×1 – y2 ×1 = x2 – y2 = (x + y) (x – y) is divisible by (x + y). Let P(k) be true for some positive integer k, i.e.,
x2k – y2k is divisible by x + y.
∴x2k – y2k = m (x + y), where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true. Consider
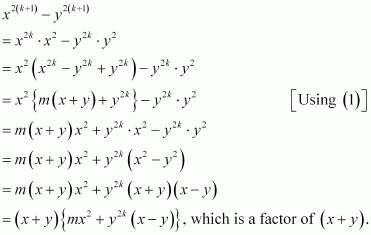
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q22 :
Prove the following by using the principle of mathematical induction for all n ∈ N: 32n + 2 - 8n - 9 is divisible by 8.
Answer :
Let the given statement be P(n), i.e., P(n): 32n + 2 – 8n – 9 is divisible by 8.
It can be observed that P(n) is true for n = 1 since 32 ×1 + 2 – 8 × 1 – 9 = 64, which is divisible by 8. Let P(k) be true for some positive integer k, i.e.,
32k+ 2 – 8k – 9 is divisible by 8.
∴32k+ 2 – 8k – 9 = 8m; where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true. Consider
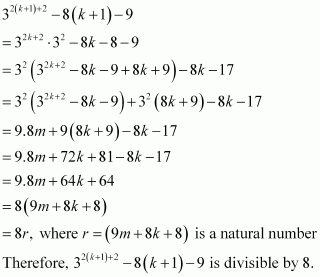
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q23 :
Prove the following by using the principle of mathematical induction for all n ∈ N: 41n - 14n is a multiple of 27.
Answer :
Let the given statement be P(n), i.e., P(n):41n – 14nis a multiple of 27.
It can be
observed that P(n) is true for n = 1 since ![]() , which is a multiple
of 27.
, which is a multiple
of 27.
Let P(k) be true for some positive integer k, i.e., 41k – 14kis a multiple of 27
∴41k – 14k = 27m, where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true. Consider
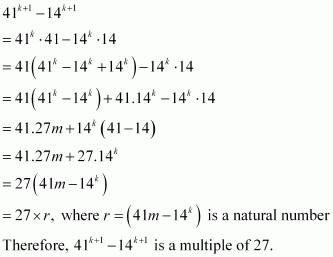
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q24 :
Prove the following by using the principle of mathematical induction
for all ![]() (2n +7) < (n + 3)2
(2n +7) < (n + 3)2
Answer :
Let the given statement be P(n), i.e., P(n): (2n +7) < (n + 3)2
It can be observed that P(n) is true for n = 1 since 2.1 + 7 = 9 < (1 + 3)2 = 16, which is true. Let P(k) be true for some positive integer k, i.e.,
(2k + 7) < (k + 3)2 … (1)
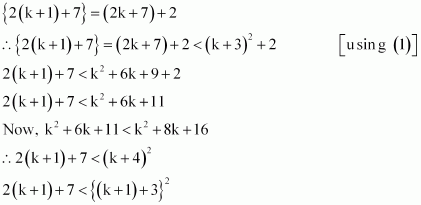 We shall now prove
that P(k + 1) is true whenever
P(k) is true.
Consider
We shall now prove
that P(k + 1) is true whenever
P(k) is true.
Consider
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.