Inverse Trignometric Functions
NCERT Textbook Solution (Laptop/Desktop is best to view this page)
www.ncrtsolutions.blogspot.com
![]() Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Exercise 2.1
![]() Question 1:
Question 1:
![]()
![]() Find the
principal value of Answer
Find the
principal value of Answer
Let sin-1 Then sin y =
![]() We know that the range of the principal value branch of sin−1 is
We know that the range of the principal value branch of sin−1 is ![]() and sin
and sin ![]()
Therefore, the principal value of
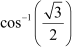 Question 2:
Question 2:
Find the principal value of Answer
We know that the range of the principal value branch of cos−1 is
![]()
![]() .
.
Therefore, the principal value of .
Question 3:
Find the principal value of cosec−1 (2) Answer
![]() Let
cosec−1 (2) = y. Then,
Let
cosec−1 (2) = y. Then,
![]()
![]() We know that the range of the principal value branch of cosec−1 is
We know that the range of the principal value branch of cosec−1 is
Therefore, the principal value of
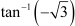 Question 4:
Question 4:
Find the principal value of Answer
We know that the range of the principal value branch of tan−1 is
![]() Therefore, the principal
value of
Therefore, the principal
value of
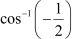 Question 5:
Question 5:
Find the principal value of Answer
We know that the range of the principal value branch of cos−1 is
![]() Therefore, the principal
value of
Therefore, the principal
value of
Question 6:
![]() Find the principal
value of tan−1 (−1) Answer
Find the principal
value of tan−1 (−1) Answer
Let tan−1 (−1) = y. Then,
We know that the range of the principal value branch of tan−1 is
![]() Therefore, the principal
value of
Therefore, the principal
value of
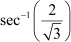 Question 7:
Question 7:
Find the principal value of Answer
We know that the range of the principal value branch of sec−1 is
![]() Therefore, the principal
value of
Therefore, the principal
value of
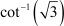 Question 8:
Question 8:
Find the principal value of Answer
We know that the range of the principal value branch of cot−1 is (0,π) and
![]() Therefore, the principal
value of
Therefore, the principal
value of
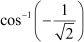 Question 9:
Question 9:
Find the principal value of Answer
We know that the range of the principal value branch of cos−1 is [0,π] and
![]()
![]() .
.
Therefore, the principal value of
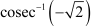 Question 10:
Question 10:
Find the principal value of Answer
We know that the range of the principal value branch of cosec−1 is
![]() Therefore, the principal
value of
Therefore, the principal
value of
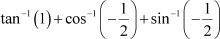 Question 11:
Question 11:
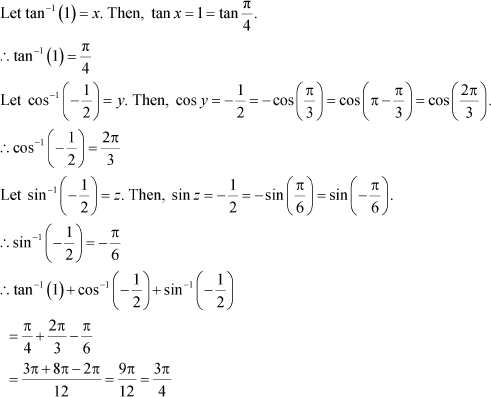 |
Find the value of Answer
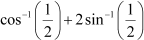 Question 12:
Question 12:
Find the value of Answer
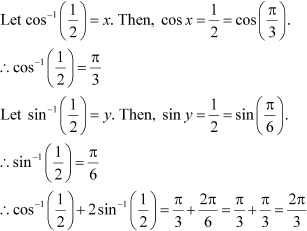
Question 13:
![]() Find the value of if sin−1 x =
y, then
Find the value of if sin−1 x =
y, then
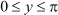
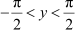 (A) (B)
(A) (B)
![]() (C) (D)
(C) (D)
Answer
It is given that sin−1 x = y.
![]() We know that the range of the principal value branch of sin−1 is
We know that the range of the principal value branch of sin−1 is ![]() Therefore, .
Therefore, .
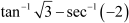 Question 14:
Question 14:
![]()
![]()
![]() Find the value of is equal to
Find the value of is equal to
(A) π (B) (C) (D) Answer
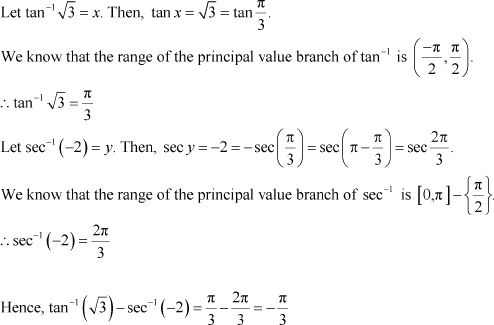
Exercise 2.2
![]() Question 1:
Question 1:
![]() Prove Answer
Prove Answer
To prove:
![]()
![]() Let x = sinθ. Then, We have,
Let x = sinθ. Then, We have,
R.H.S. =
= 3θ
= L.H.S.
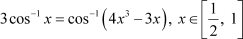 Question 2:
Question 2:
![]() Prove Answer
Prove Answer
To prove:
Let x = cosθ. Then, cos−1 x =θ. We have,
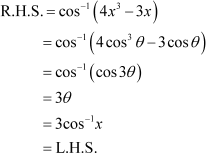
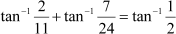 Question 3:
Question 3:
![]() Prove Answer
Prove Answer
To prove:
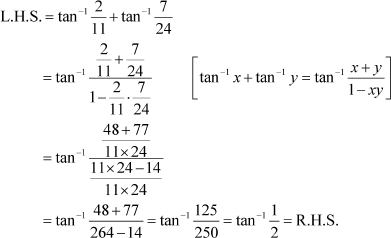 |
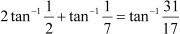 Question 4:
Question 4:
![]() Prove Answer
Prove Answer
To prove:
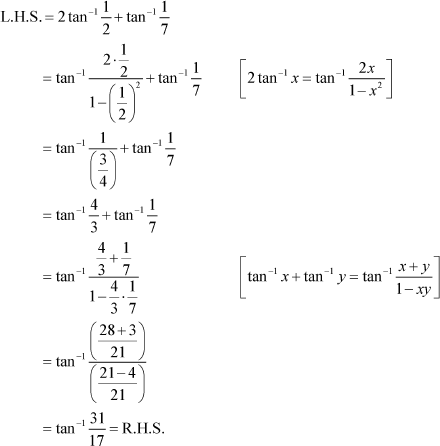
Question 5:
Write the function in the simplest form:
Answer
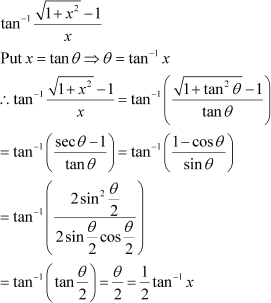
Question 6:
Write the function in the simplest form:
Answer
Put x = cosec θ ⇒ θ = cosec−1 x
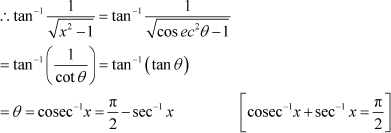 |
Question 7:
Write the function in the simplest form:
![]()
Answer
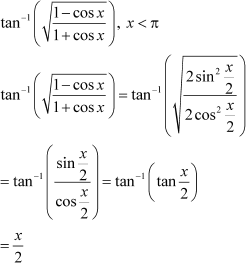 |
Question 8:
Write the function in the simplest form:
Answer
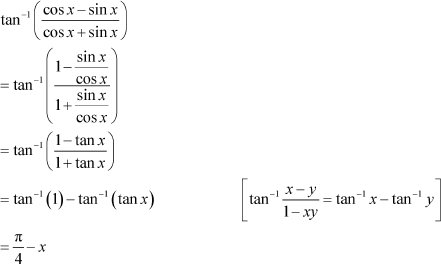 |
Question 9:
Write the function in the simplest form:
Answer
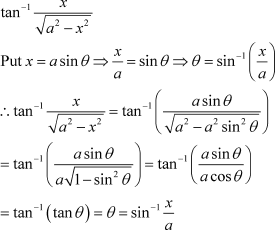 |
Question 10:
Write the function in the simplest form:
Answer
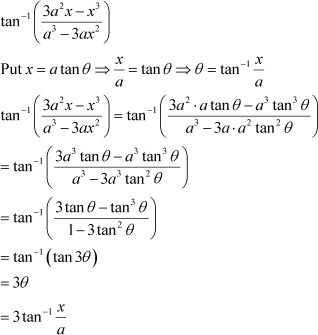
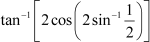 Question 11:
Question 11:
![]()
![]() Find the value of Answer
Find the value of Answer
Let . Then,
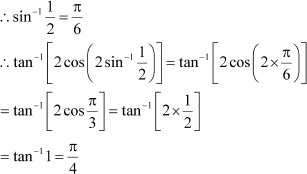 |
Question 12:
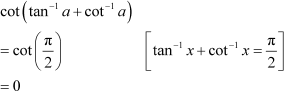 |
Question 13:
![]() Find the value of Answer
Find the value of Answer
Let x = tan θ. Then, θ = tan−1 x.
Let y = tan Φ. Then, Φ = tan−1 y.
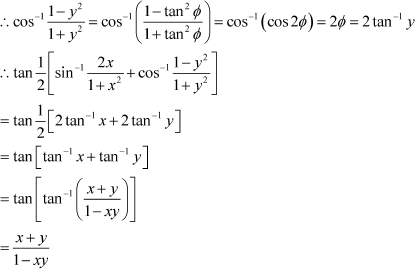 |
Question 14:
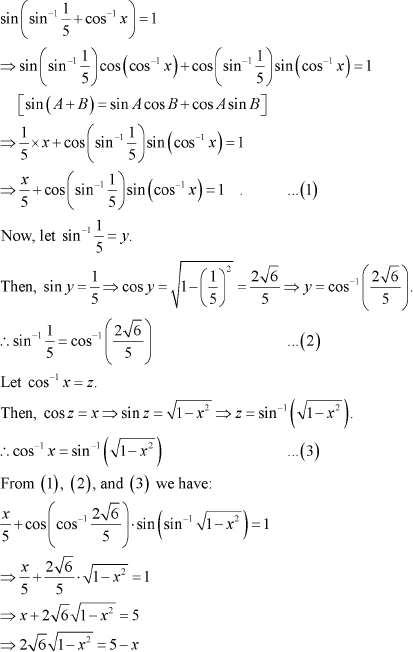 |
On squaring both sides, we get:
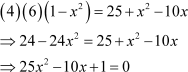
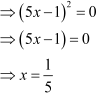 |
![]() Hence, the value of x is
Hence, the value of x is
Question 15:
![]() If , then find the value of x.
If , then find the value of x.
Answer
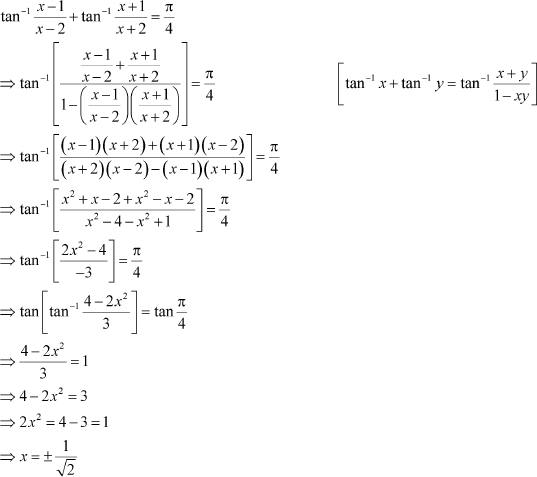
![]() Hence, the value of x is
Hence, the value of x is
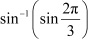 Question 16:
Question 16:
Find the values of Answer
![]()
![]() We know that sin−1 (sin x) = x
if , which is the principal
value branch of sin−1x.
We know that sin−1 (sin x) = x
if , which is the principal
value branch of sin−1x.
![]() Here,
Here,
Now, can be written as:
 Question 17:
Question 17:
Find the values of Answer
![]()
![]() We know that tan−1 (tan x) = x
if , which is the principal value branch of tan−1x.
We know that tan−1 (tan x) = x
if , which is the principal value branch of tan−1x.
![]() Here,
Here,
Now, can be written as:
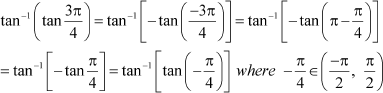 |
![]()
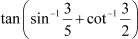 Question 18:
Question 18:
![]()
![]() Find the values of Answer
Find the values of Answer
Let . Then,
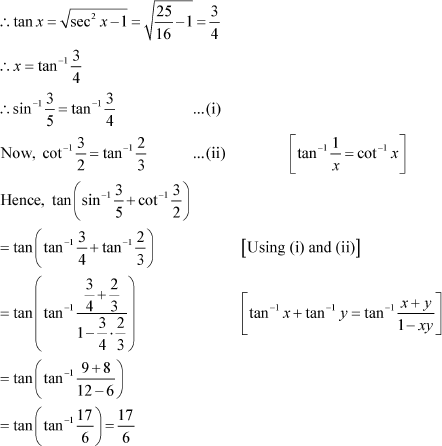 |
Question 19:
![]() Find the values of is equal to
Find the values of is equal to
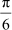 (A)
(A) 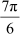 (B)
(B) 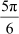 (C)
(C) 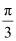 (D)
(D)
Answer
![]() We know that
cos−1 (cos x) = x if , which is the principal
value branch of cos
We know that
cos−1 (cos x) = x if , which is the principal
value branch of cos
![]() −1x.
−1x.
![]() Here,
Here,
Now, can be written as:
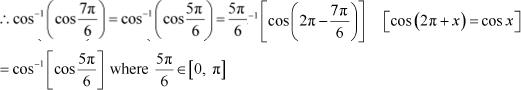 |
The correct answer is B.
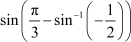 Question 20:
Question 20:
Find the values of is equal to
(A) 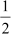 (B)
(B) 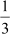 (C)
(C) 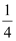 (D) 1
(D) 1
![]()
![]() Answer
Answer
![]() Let . Then,
Let . Then,
We know that the range of the principal value branch of .
![]() ∴
∴
The correct answer is D.
Miscellaneous Solutions
![]() Question 1:
Question 1:
![]() Find the value of Answer
Find the value of Answer
We know that cos−1 (cos x) = x if , which is the principal value branch of cos
![]() −1x.
−1x.
![]() Here,
Here,
Now, can be written as:
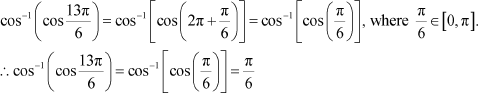 |
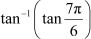 Question 2:
Question 2:
![]() Find the value of Answer
Find the value of Answer
![]() We know that tan−1 (tan x) = x
if , which is the principal value branch of tan −1x.
We know that tan−1 (tan x) = x
if , which is the principal value branch of tan −1x.
![]() Here,
Here,
Now, can be written as:
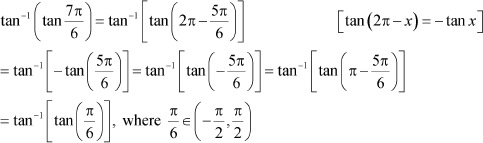
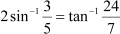 Question 3:
Question 3:
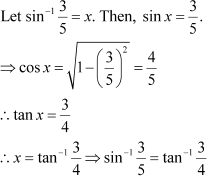 |
Prove Answer
Now, we have:
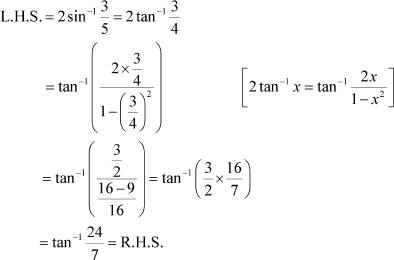
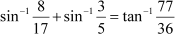 Question 4:
Question 4:
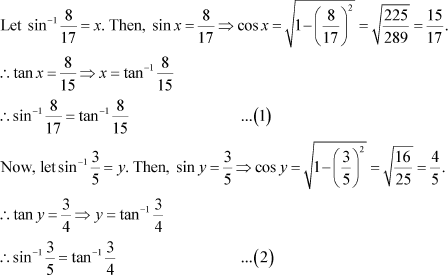 |
Prove Answer
Now, we have:
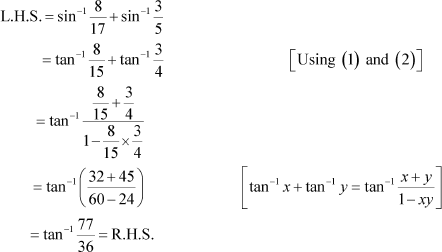
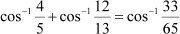 Question 5:
Question 5:
Prove Answer
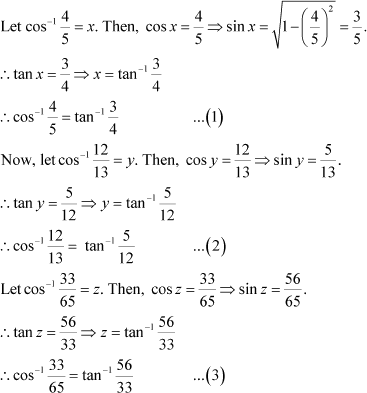
Now, we will prove that:
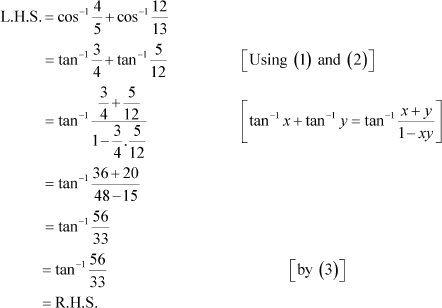 |
 Question 6:
Question 6:
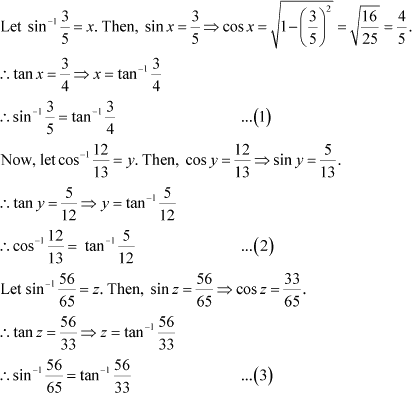 |
Prove Answer
Now, we have:
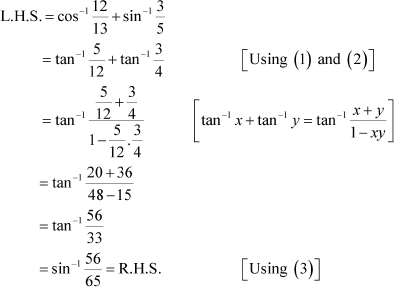
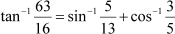 Question 7:
Question 7:
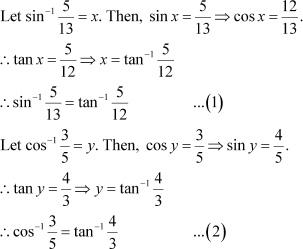 |
Prove Answer
Using (1) and (2), we have
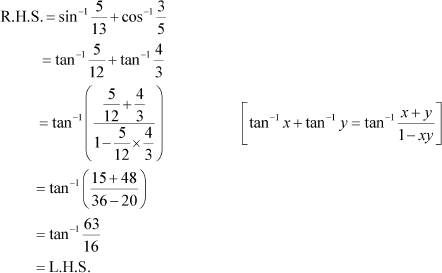
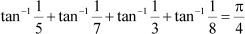 Question 8:
Question 8:
Prove Answer
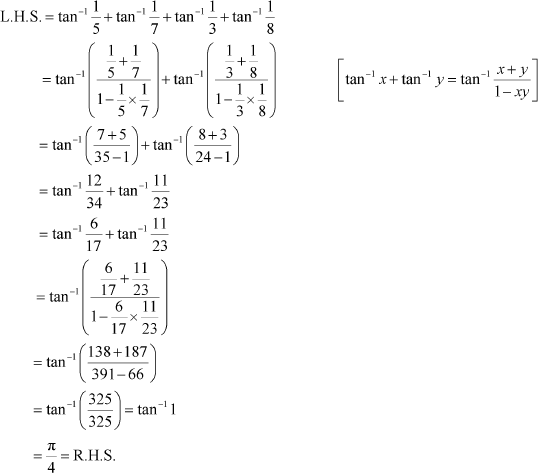
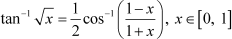 Question 9:
Question 9:
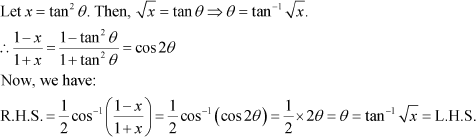 |
Prove Answer
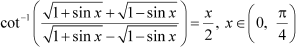 Question 10:
Question 10:
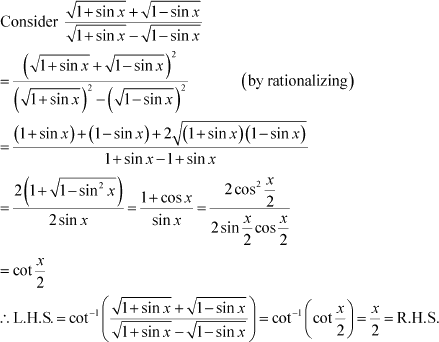 |
Prove Answer
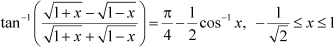 Question 11:
Question 11:
Prove [Hint: putx = cos 2θ]
Answer
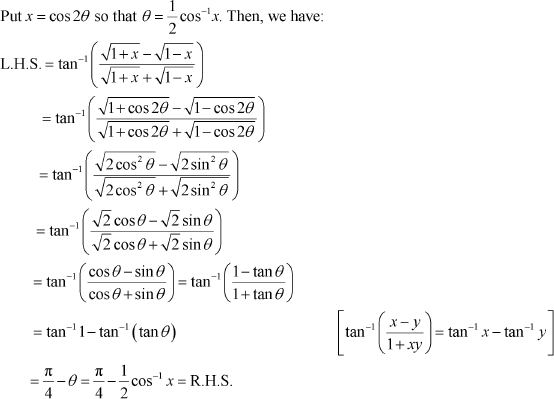
Question 12:
Prove ![]() Answer
Answer
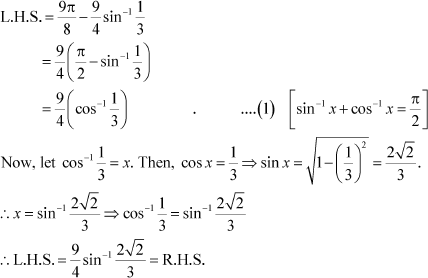
Question 13:
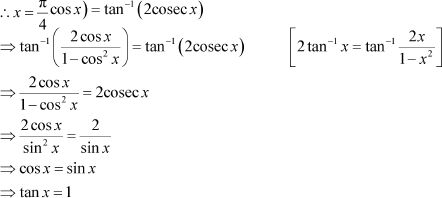 |
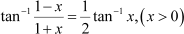 Question 14:
Question 14:
Solve Answer
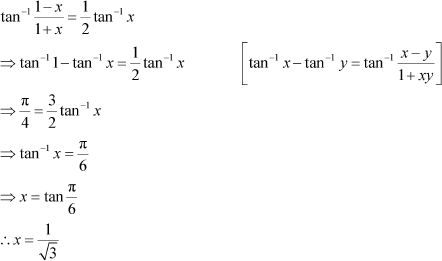
Question 15:
![]()
![]()
![]()
![]() Solve
Solve ![]() is equal to
is equal to
![]() (A) (B) (C) (D) Answer
(A) (B) (C) (D) Answer
Let tan−1 x = y. Then,
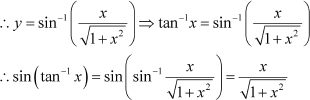 |
The correct answer is D.
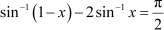 Question 16:
Question 16:
Solve , then x is equal to
![]()
![]()
![]() (A) (B) (C) 0
(D)
(A) (B) (C) 0
(D)
Answer
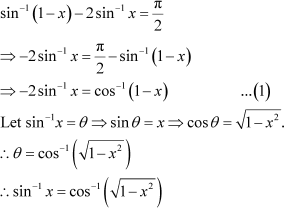 |
Therefore, from equation (1), we have
Put x = sin y. Then, we have:
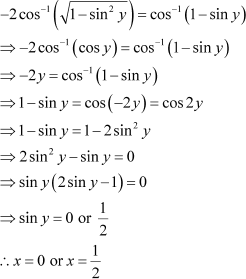 |
![]() But, when , it can be observed that:
But, when , it can be observed that:
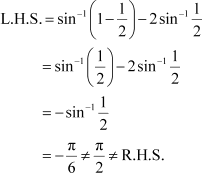
![]() is not the solution
of the given equation.
is not the solution
of the given equation.
Thus, x = 0.
Hence, the correct answer is C.
Question 17:
Solve ![]() is equal to
is equal to
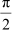
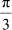 (A) (B). (C)
(A) (B). (C) 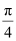 (D)
(D) 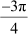
Answer
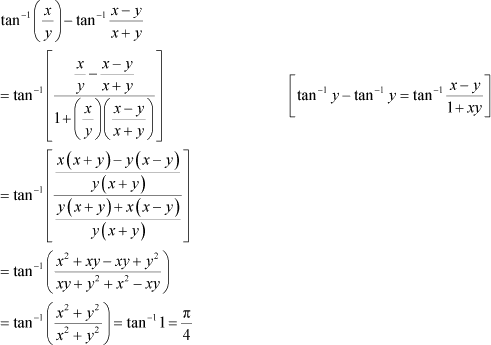
Hence, the correct answer is C.