Differentials Equations
NCERT Textbook Solution (Laptop/Desktop is best to view this page)
![]() Class XII Chapter 9 – Differential Equations Maths
Class XII Chapter 9 – Differential Equations Maths
![]()
www.ncrtsolutions.blogspot.com
Exercise 9.1
Question 1:
Determine order
and degree(if defined)
of differential equation ![]() Answer
Answer
 |
The highest
order derivative present
in the differential equation is ![]() . Therefore, its order is four.
. Therefore, its order is four.
The given differential equation is not a polynomial equation in its derivatives. Hence, its degree is not defined.
Question 2:
Determine order
and degree(if defined)
of differential equation
![]() Answer
Answer
The given differential equation is:
The highest
order derivative present
in the differential equation is ![]() . Therefore, its order is one.
. Therefore, its order is one.
It is a polynomial equation in ![]() . The highest power raised to
. The highest power raised to ![]() is 1. Hence, its degree is one.
is 1. Hence, its degree is one.
Question 3:
Page 1 of 120
![]() The highest
order derivative present
in the given differential equation
is . Therefore, its order
is two.
The highest
order derivative present
in the given differential equation
is . Therefore, its order
is two.
It is a polynomial equation in ![]() and
and ![]() . The power raised to
. The power raised to ![]() is 1. Hence, its degree is one.
is 1. Hence, its degree is one.
Question 4:
The highest order derivative present in the given differential equation is ![]() . Therefore, its order is 2.
. Therefore, its order is 2.
The given differential equation is not a polynomial equation in its derivatives. Hence, its degree is not defined.
Question 5:
Determine order and degree(if defined) of differential equation
The highest
order derivative present
in the differential equation is ![]() . Therefore, its order is two.
. Therefore, its order is two.
![]()
![]() It is a polynomial equation in and the power raised to is 1. Hence, its degree is one.
It is a polynomial equation in and the power raised to is 1. Hence, its degree is one.
Question 6:
Determine order and degree(if defined) of differential equation
Answer
The highest order
derivative present in the differential equation is ![]() . Therefore, its order is three.
. Therefore, its order is three.
The given differential equation
is a polynomial equation in ![]() . The highest power
raised to
. The highest power
raised to ![]() is 2. Hence, its degree is 2.
is 2. Hence, its degree is 2.
Question 7:
![]() Determine order and degree(if defined) of differential equation
Determine order and degree(if defined) of differential equation ![]() Answer
Answer
The highest
order derivative present
in the differential equation is ![]() . Therefore, its order is three.
. Therefore, its order is three.
It is a polynomial equation in ![]() . The highest power raised to
. The highest power raised to ![]() is 1. Hence, its degree is 1.
is 1. Hence, its degree is 1.
Question 8:
Determine order and degree(if defined) of differential equation
The highest
order derivative present
in the differential equation is ![]() . Therefore, its order is one.
. Therefore, its order is one.
The given differential equation
is a polynomial equation in ![]() and the highest power
raised to
and the highest power
raised to ![]() is one. Hence,
its degree is one.
is one. Hence,
its degree is one.
Question 9:
Determine order and degree(if defined) of differential equation
The highest
order derivative present
in the differential equation is ![]() . Therefore, its order
is two.
. Therefore, its order
is two.
The given differential equation
is a polynomial equation in ![]() and
and ![]() and the highest
and the highest
power raised to ![]() is one. Hence, its degree is one.
is one. Hence, its degree is one.
Question 10:
Determine order and degree(if defined) of differential equation
The highest
order derivative present
in the differential equation is ![]() . Therefore, its order
is two.
. Therefore, its order
is two.
This is a polynomial equation in ![]() and
and ![]() and the highest power
raised to
and the highest power
raised to ![]() is one. Hence, its degree is one.
is one. Hence, its degree is one.
Question 11:
![]() The degree of the differential equation
The degree of the differential equation
is
(A) 3 (B) 2 (C) 1 (D) not defined Answer
The given differential equation is not a polynomial equation in its derivatives. Therefore, its degree is not defined.
Hence, the correct answer is D.
Question 12:
![]() The order of the differential equation
The order of the differential equation
is
(A) 2 (B) 1 (C) 0 (D) not defined Answer
The highest
order derivative present
in the given differential equation
is ![]() . Therefore, its order is two.
. Therefore, its order is two.
Hence, the correct answer is A.
Exercise 9.2
Question 1:
Answer
Differentiating both sides of this equation with respect to x, we get:
 |
Now, differentiating equation (1) with respect to x, we get:
 |
Substituting the values of
Thus, the given function is the solution of the corresponding differential equation.
Question 2:
Answer
Differentiating both sides of this equation with respect to x, we get:
 |
Substituting the value of ![]() in the given differential equation, we get:
in the given differential equation, we get:
L.H.S. = ![]() = R.H.S.
= R.H.S.
Hence, the given function is the solution of the corresponding differential equation.
Question 3:
Answer
Differentiating both sides of this equation with respect to x, we get:
 |
Substituting the value of ![]() in the given differential equation, we get:
in the given differential equation, we get:
L.H.S. = ![]() = R.H.S.
= R.H.S.
Hence, the given function is the solution of the corresponding differential equation.
Question 4:
Answer
Differentiating both sides of the equation with respect to x, we get:

![]() L.H.S. = R.H.S.
L.H.S. = R.H.S.
Hence, the given function is the solution of the corresponding differential equation.
Question 5:
Answer
Differentiating both sides with respect to x, we get:
 |
Substituting the value of
Hence, the given function is the solution of the corresponding differential equation.
Question 6:
Answer
Differentiating both sides of this equation with respect to x, we get:
 |
Substituting the value of ![]() in the given differential equation, we get:
in the given differential equation, we get:
 |
Hence, the given function is the solution of the corresponding differential equation.
Question 7:
Answer
Differentiating both sides of this equation with respect to x, we get:

![]() L.H.S. = R.H.S.
L.H.S. = R.H.S.
Hence, the given function is the solution of the corresponding differential equation.
Question 8:
Answer
Differentiating both sides of the equation with respect to x, we get:
 |
![]() Substituting the value of in
equation (1), we get:
Substituting the value of in
equation (1), we get:

Hence, the given function is the solution of the corresponding differential equation.
Question 9:
Answer
Differentiating both sides of this equation with respect to x, we get:
 |
Substituting the value of ![]() in the given differential equation, we get:
in the given differential equation, we get:

Hence, the given function is the solution of the corresponding differential equation.
Question 10:
Answer
Differentiating both sides of this equation with respect to x, we get:
 |
Substituting the value of ![]() in the given differential equation, we get:
in the given differential equation, we get:
 |
Hence, the given function is the solution of the corresponding differential equation.
Question 11:
The numbers of arbitrary constants in the general solution of a differential equation of fourth order are:
(A) 0 (B) 2 (C) 3 (D) 4
Answer
We know that the number of constants in the general solution of a differential equation of order n is equal to its order.
Therefore, the number of constants in the general equation of fourth order differential equation is four.
Hence, the correct answer is D.
Question 12:
The numbers of arbitrary constants in the particular solution of a differential equation of third order are:
(A) 3 (B) 2 (C) 1 (D) 0
Answer
In a particular solution of a differential equation, there are no arbitrary constants. Hence, the correct answer is D.
Exercise 9.3
Question 1:
Answer
Differentiating both sides of the given equation with respect to x, we get:
 |
Again, differentiating both sides with respect to x, we get:
 |
Hence, the required differential equation of the given curve
is ![]()
Question 2:
Answer
Differentiating both sides with respect to x, we get:
 |
Again, differentiating both sides with respect to x, we get:
![]()
Dividing equation (2) by equation (1), we get:
 |
This is the required differential equation of the given curve.
Question 3:
Answer
Differentiating both sides with respect to x, we get:
Again, differentiating both sides with respect to x, we get:
Multiplying equation (1) with (2) and then adding it to equation (2), we get:
 |
Now, multiplying equation (1) with equation (3) and subtracting equation (2) from it, we get:

Substituting the values
of ![]() in equation
(3), we get:
in equation
(3), we get:

This is the required differential equation of the given curve.
Question 4:
Answer
Differentiating both sides with respect to x, we get:
Multiplying equation (1) with equation (2) and then subtracting it from equation (2), we get:
![]()
Differentiating both sides with respect to x, we get:
Dividing equation (4) by equation (3), we get:
 |
This is the required differential equation of the given curve.
Question 5:
Answer
Differentiating both sides with respect to x, we get:
Again, differentiating with respect to x, we get:
 |
Adding equations (1) and (3), we get:
 |
This is the required differential equation of the given curve.
Question 6:
Form the differential equation of the family of circles touching the y-axis at the origin. Answer
The centre of the circle touching the y-axis at origin lies on the x-axis. Let (a, 0) be the centre of the circle.
Since it touches the y-axis at origin, its radius is a.
Now, the equation of the circle with centre (a, 0) and radius (a) is

Differentiating equation (1) with respect to x, we get:
Now, on substituting the value of a in equation (1), we get:
 |
This is the required differential equation.
Question 7:
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Answer
The equation of the parabola having the vertex at origin and the axis along the positive
y-axis is:

Differentiating equation (1) with respect to x, we get:
Dividing equation (2) by equation (1), we get:
 |
This is the required differential equation.
Question 8:
Form the differential equation of the family of ellipses having foci on y-axis and centre at origin.
Answer
The equation of the family of ellipses having foci on the y-axis and the centre at origin is as follows:

Differentiating equation (1) with respect to x, we get:
 |
Again, differentiating with respect to x, we get:
 |
Substituting this value in equation (2), we get:
 |
This is the required differential equation.
Question 9:
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.
Answer
 |
The equation of the family of hyperbolas with the centre at origin and foci along the x- axis is:
Differentiating both sides of equation (1) with respect to x, we get:
 |
Again, differentiating both sides with respect to x, we get:
 |
![]() Substituting the value of in equation (2), we get:
Substituting the value of in equation (2), we get:
 |
This is the required differential equation.
Question 10:
Form the differential equation of the family of circles having centre on y-axis and radius 3 units.
Answer
Let the centre of the circle on y-axis be (0, b).
 |
The differential equation of the family of circles with centre at (0, b) and radius 3 is as follows:
Differentiating equation (1) with respect to x, we get:
 |
Substituting the value of (y – b) in equation (1), we get:

This is the required differential equation.
Question 11:
Which of the following
differential equations has ![]() as the general solution?
as the general solution?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Answer
The given equation is:
Differentiating with respect to x, we get:
Again, differentiating with respect to x, we get:

This is the required differential equation of the given equation of curve. Hence, the correct answer is B.
Question 12:
![]() Which of the following differential equation has as one of its particular solution?
Which of the following differential equation has as one of its particular solution?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Answer
The given equation of curve is y = x. Differentiating with respect to x, we get:
Again, differentiating with respect to x, we get:
Now, on substituting the values of y, ![]() from equation
(1) and (2) in each of
from equation
(1) and (2) in each of
the given alternatives, we find that only the differential equation given in alternative C is correct.

Hence, the correct answer is C.
Exercise 9.4
Question 1:
Answer
The given differential equation is:
 |
Now, integrating both sides of this equation, we get:
 |
This is the required general solution of the given differential equation.
Question 2:
Answer
The given differential equation is:

Now, integrating both sides of this equation, we get:
 |
This is the required general solution of the given differential equation.
Question 3:
Answer
The given differential equation is:
 |
Now, integrating both sides, we get:

This is the required general solution of the given differential equation.
Question 4:
Answer
The given differential equation is:
 |
Integrating both sides of this equation, we get:

Substituting these values in equation (1), we get:
 |
This is the required general solution of the given differential equation.
Question 5:
Answer
The given differential equation is:
 |
Integrating both sides of this equation, we get:

Let (ex + e–x) = t.
Differentiating both sides with respect to x, we get:
 |
Substituting this value in equation (1), we get:
 |
This is the required general solution of the given differential equation.
Question 6:
Answer
The given differential equation is:
 |
Integrating both sides of this equation, we get:

This is the required general solution of the given differential equation.
Question 7:
Answer
The given differential equation is:
 |
Integrating both sides, we get:
 |
Substituting this value in equation (1), we get:

This is the required general solution of the given differential equation.
Question 8:
Answer
The given differential equation is:
 |
Integrating both sides, we get:
 |
This is the required general solution of the given differential equation.
Question 9:
Answer
The given differential equation is:
 |
Integrating both sides, we get:
 |
Substituting this value in equation (1), we get:

This is the required general solution of the given differential equation.
Question 10:
Answer
The given differential equation is:
 |
Integrating both sides, we get:
 |

![]() Substituting the values of in equation
(1), we get:
Substituting the values of in equation
(1), we get:
 |
This is the required general solution of the given differential equation.
Question 11:
Answer
The given differential equation is:
 |
Integrating both sides, we get:

Comparing the coefficients of x2 and x, we get:
A + B = 2 B + C = 1 A + C = 0
Solving these equations, we get:
Substituting the values of A, B, and C in equation (2), we get:
Therefore, equation (1) becomes:

Substituting C = 1 in equation (3), we get:
Question 12:
Answer
 |
Integrating both sides, we get:

Comparing the coefficients of x2, x, and constant, we get:
 |
Solving these equations, we get
![]() Substituting the values of A, B, and C in equation
(2), we get:
Substituting the values of A, B, and C in equation
(2), we get:
![]()
Therefore, equation (1) becomes:

Substituting the value of k2 in equation (3), we get:
 |
Question 13:
Answer

Integrating both sides, we get:
 |
Substituting C = 1 in equation (1), we get:
 |
Question 14:
Answer
 |
Integrating both sides, we get:

Substituting C = 1 in equation (1), we get:
y = sec x
Question 15:
Find the equation of a curve passing through the point (0, 0) and whose differential
equation is ![]() .
.
Answer
The differential equation of the curve is:
 |
Integrating both sides, we get:
 |

Substituting this value in equation (1), we get:
Now, the curve passes through point (0, 0).
 |
 |
Substituting
Hence, the required equation
of the curve is ![]()
Question 16:
For the differential equation
![]() find the solution curve passing through
the point (1, –1).
find the solution curve passing through
the point (1, –1).
Answer
The differential equation of the given curve is:
 |
Integrating both sides, we get:
 |
Now, the curve passes through point (1, –1).
 |
Substituting C = –2 in equation (1), we get:
This is the required solution of the given curve.
Question 17:
Find the equation of a curve passing through the point (0, –2) given that at any point
![]() on the curve,
the product of the slope of its tangent and y-coordinate of the point
is equal to the x-coordinate of the
point.
on the curve,
the product of the slope of its tangent and y-coordinate of the point
is equal to the x-coordinate of the
point.
Answer
Let x and y be the x-coordinate and y-coordinate of the curve respectively.
![]() We know that the slope of a tangent
to the curve in the coordinate axis is
given by the
We know that the slope of a tangent
to the curve in the coordinate axis is
given by the
According to the given information, we get:
 |
Integrating both sides, we get:
 |
Now, the curve passes through point (0, –2).
∴ (–2)2 – 02 = 2C
⇒ 2C = 4
Substituting 2C = 4 in equation (1), we get:
y2 – x2 = 4
This is the required equation of the curve.
Question 18:
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (–4, –3). Find the equation of the curve given that it passes through (–2, 1).
Answer
It is given that (x, y) is the point of contact of the curve and its tangent.
The slope (m1) of the line segment joining
(x, y) and (–4, –3) is ![]()
We know that the slope of the tangent
to the curve is given
by the relation, ![]()
According to the given information:
 |
Integrating both sides, we get:
 |
This is the general equation of the curve.
It is given that it passes through point (–2, 1).
 |
Substituting C = 1 in equation (1), we get:
y + 3 = (x + 4)2
This is the required equation of the curve.
Question 19:
The volume of spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds.
Answer
Let the rate of change of the volume of the balloon be k (where k is a constant).
 |
Integrating both sides, we get:
 |
⇒ 4π × 33 = 3 (k × 0 + C)
⇒ 108π = 3C
⇒ C = 36π
At t = 3, r = 6:
⇒ 4π × 63 = 3 (k × 3 + C)
⇒ 864π = 3 (3k + 36π)
⇒ 3k = –288π – 36π = 252π
⇒ k = 84π
Substituting the values of k and C in equation (1), we get:
 |
Thus, the radius of the balloon
after t seconds is ![]() .
.
Question 20:
In a bank, principal increases continuously at the rate of r% per year. Find the value of r
if Rs 100 doubles itself in 10 years (loge 2 = 0.6931).
Answer
 |
Let p, t, and r represent the principal, time, and rate of interest respectively. It is given that the principal increases continuously at the rate of r% per year.
Integrating both sides, we get:
 |
It is given that when t = 0, p = 100.
⇒ 100 = ek … (2)
 |
Now, if t = 10, then p = 2 × 100 = 200. Therefore, equation (1) becomes:
Hence, the value of r is 6.93%.
Question 21:
In a bank, principal increases continuously at the rate of 5% per year. An amount of Rs
1000 is deposited with this bank,
how much will it worth
after 10 years ![]() . Answer
. Answer
Let p and t be the principal and time respectively.
It is given that the principal increases continuously at the rate of 5% per year.
 |
Integrating both sides, we get:
 |
Now, when t = 0, p = 1000.
⇒ 1000 = eC … (2)
At t = 10, equation (1) becomes:
 |
Hence, after 10 years the amount will worth Rs 1648.
Question 22:
In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present?
Answer
Let y be the number of bacteria at any instant t.
It is given that the rate of growth of the bacteria is proportional to the number present.
 |
Integrating both sides, we get:
 |
Let y0 be the number of bacteria at t = 0.
⇒ log y0 = C
Substituting the value of C in equation (1), we get:
 |
Also, it is given that the number of bacteria increases by 10% in 2 hours.

Substituting this value in equation (2), we get:
Therefore, equation (2) becomes:
Now, let the time when the number of bacteria increases from 100000 to 200000 be t1.
⇒ y = 2y0 at t = t1
From equation (4), we get:
![]() Hence, in hours the number of bacteria increases
from 100000 to 200000.
Hence, in hours the number of bacteria increases
from 100000 to 200000.
Question 23:
The general
solution of the differential equation
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Answer
Integrating both sides, we get:
Hence, the correct answer is A.
Exercise 9.5
Question 1:
Answer
The given differential equation i.e., (x2 + xy) dy = (x2 + y2) dx can be written as:
This shows that equation (1) is a homogeneous equation. To solve it, we make the substitution as:
y = vx
Differentiating both sides with respect to x, we get:
![]() Substituting the values of v and in equation (1), we get:
Substituting the values of v and in equation (1), we get:

Integrating both sides, we get:
This is the required solution of the given differential equation.
Question 2:
Answer
The given differential equation is:
Thus, the given equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx
Differentiating both sides with respect to x, we get:
Substituting the values of y and
Integrating both sides, we get:
This is the required solution of the given differential equation.
Question 3:
Answer
The given differential equation is:
Thus, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx
![]() Substituting the values of y and in equation (1), we get:
Substituting the values of y and in equation (1), we get:
Integrating both sides, we get:
This is the required solution of the given differential equation.
Question 4:
Answer
The given differential equation is:
Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx

![]() Substituting the values of y and in equation (1), we get:
Substituting the values of y and in equation (1), we get:
Integrating both sides, we get:
This is the required solution of the given differential equation.
Question 5:
Answer
The given differential equation is:

Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx
Substituting the values of y and
Integrating both sides, we get:

This is the required solution for the given differential equation.
Question 6:
Answer
Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx
Substituting the values of v and
![]() in equation
(1), we get:
in equation
(1), we get:

Integrating both sides, we get:
This is the required solution of the given differential equation.
Question 7:
Answer
The given differential equation is:

Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx
![]() Substituting the values of y and in equation (1), we get:
Substituting the values of y and in equation (1), we get:

Integrating both sides, we get:
This is the required solution of the given differential equation.
Question 8:
Answer
Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx
![]() Substituting the values of y and in equation (1), we get:
Substituting the values of y and in equation (1), we get:
Integrating both sides, we get:
This is the required solution of the given differential equation.
Question 9:
Answer
Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx

Substituting the values
of y and
![]() in equation
(1), we get:
in equation
(1), we get:

Integrating both sides, we get:

Therefore, equation (1) becomes:
This is the required solution of the given differential equation.
Question 10:
Answer

Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
x = vy
Substituting the values of x and
![]() in equation
(1), we get:
in equation
(1), we get:

Integrating both sides, we get:

This is the required solution of the given differential equation.
Question 11:
Answer
Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx
![]() Substituting the values of y and in equation (1), we get:
Substituting the values of y and in equation (1), we get:

Integrating both sides, we get:
Now, y = 1 at x = 1.
Substituting the value of 2k in equation (2), we get:
This is the required solution of the given differential equation.
Question 12:
Answer
Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx
![]() Substituting the values of y and in equation (1), we get:
Substituting the values of y and in equation (1), we get:
Integrating both sides, we get:
Now, y = 1 at x = 1.
![]() in equation
(2), we get:
in equation
(2), we get:
This is the required solution of the given differential equation.
Question 13:
Answer
Therefore, the given differential equation is a homogeneous equation. To solve this differential equation, we make the substitution as:
y = vx
Substituting the values of y and
Integrating both sides, we get:

![]() Now,
Now,
.
Substituting C = e in equation (2), we get:
This is the required solution of the given differential equation.
Question 14:
Answer
Therefore, the given differential equation is a homogeneous equation.
To solve it, we make the substitution as:
y = vx
Substituting the values of y and
Integrating both sides, we get:
This is the required solution of the given differential equation. Now, y = 0 at x = 1.

Substituting C = e in equation (2), we get:
This is the required solution of the given differential equation.
Question 15:
Answer
Therefore, the given differential equation is a homogeneous equation. To solve it, we make the substitution as:
y = vx
Substituting the value of y and
Integrating both sides, we get:

Now, y = 2 at x = 1.
Substituting C = –1 in equation (2), we get:
This is the required solution of the given differential equation.
Question 16:
![]() A homogeneous differential equation of the form can be solved by making the substitution
A homogeneous differential equation of the form can be solved by making the substitution
A. y = vx
B. v = yx
C. x = vy
D. x = v
Answer
![]() For solving
the homogeneous equation
of the form , we need to make the substitution as x = vy.
For solving
the homogeneous equation
of the form , we need to make the substitution as x = vy.
Hence, the correct answer is C.
Question 17:
Which of the following is a homogeneous differential equation?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Answer
Function F(x, y) is said to be the homogenous function of degree n, if F(λx, λy) = λn F(x, y) for any non-zero constant (λ).
Consider the equation given in alternativeD:
Hence, the differential equation given in alternative D is a homogenous equation.
Exercise 9.6
Question 1:
Answer
The given differential equation
is ![]()
This is in the form
of ![]()
The solution of the given differential equation is given by the relation,
Therefore, equation (1) becomes:
This is the required general solution of the given differential equation.
Question 2:
Answer
The given differential equation is
The solution of the given differential equation is given by the relation,
This is the required general solution of the given differential equation.
Question 3:
Answer
The given differential equation is:
The solution of the given differential equation is given by the relation,
This is the required general solution of the given differential equation.
Question 4:
Answer
The given differential equation is:
The general solution of the given differential equation is given by the relation,
Question 5:
Answer

By second fundamental theorem of calculus, we obtain
Question 6:
Answer
The given differential equation is:
This equation is in the form of a linear differential equation as:
The general solution of the given differential equation is given by the relation,

Question 7:
Answer
The given differential equation is:
This equation is the form of a linear differential equation as:
The general solution of the given differential equation is given by the relation,

![]() Substituting the value of in equation
(1), we get:
Substituting the value of in equation
(1), we get:
This is the required general solution of the given differential equation.
Question 8:
Answer
This equation is a linear differential equation of the form:
The general solution of the given differential equation is given by the relation,
Question 9:
Answer
This equation is a linear differential equation of the form:
The general solution of the given differential equation is given by the relation,

Question 10:
Answer
This is a linear differential equation of the form:
The general solution of the given differential equation is given by the relation,

Question 11:
Answer
This is a linear differential equation of the form:
The general solution of the given differential equation is given by the relation,

Question 12:
Answer
This is a linear differential equation of the form:
The general solution of the given differential equation is given by the relation,

Question 13:
Answer
The given differential equation is
The general solution of the given differential equation is given by the relation,
Now,
Substituting C = –2 in equation (1), we get:
![]()
Hence, the required solution
of the given differential equation
is ![]()
Question 14:
Answer
This is a linear differential equation of the form:
The general solution of the given differential equation is given by the relation,
Now, y = 0 at x = 1. Therefore,

Substituting ![]() in equation
(1), we get:
in equation
(1), we get:
This is the required general solution of the given differential equation.
Question 15:
Answer
The given differential equation is
The general solution of the given differential equation is given by the relation,
Now,
Substituting C = 4 in equation (1), we get:
This is the required particular solution of the given differential equation.
Question 16:
Find the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the coordinates of the point.
Answer
Let F (x, y) be the curve passing through the origin.
At point
(x, y), the slope of the curve will be ![]() According to the given information:
According to the given information:
This is a linear differential equation of the form:
The general solution of the given differential equation is given by the relation,
Substituting in equation (1), we get:
The curve passes through the origin. Therefore, equation (2) becomes:
1 = C
Substituting C = 1 in equation (2), we get:
⇒ ![]()
Hence, the required equation
of curve passing
through the origin
is ![]()
Question 17:
Find the equation of a curve passing through the point (0, 2) given that the sum of the coordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.
Answer
Let F (x, y) be the curve and let (x, y) be a point on the curve. The slope of the tangent
to the curve at (x, y) is
This is a linear differential equation of the form:

The general equation of the curve is given by the relation,
Therefore, equation (1) becomes:
The curve passes through point (0, 2). Therefore, equation (2) becomes:
0 + 2 – 4 = Ce0
⇒ – 2 = C
⇒ C = – 2
Substituting C = –2 in equation (2), we get:
This is the required equation of the curve.
Question 18:
The integrating factor of the differential equation ![]() is
is
A. e–x
B. e–y
C. ![]()
D. x
Answer
The given differential equation is:
This is a linear differential equation of the form:
The integrating factor (I.F) is given by the relation,
Hence, the correct answer is C.
Question 19:
The integrating factor of the differential equation.
![]() is
is
![]() A.
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
Answer
The given differential equation is:
This is a linear differential equation of the form:
The integrating factor (I.F) is given by the relation,
Hence, the correct answer is D.
Miscellaneous Solutions
Question 1:
For each of the differential equations given below, indicate its order and degree (if defined).
(i) ![]()
(ii) ![]()
(iii) ![]()
Answer
(i) The differential equation is given as:
The highest order
derivative present in the differential equation is ![]() . Thus, its order is two. The highest
power raised to
. Thus, its order is two. The highest
power raised to ![]() is one. Hence, its degree is one.
is one. Hence, its degree is one.
(ii)
The differential equation is given as:
![]() The highest
order derivative present
in the differential equation is . Thus, its order is
The highest
order derivative present
in the differential equation is . Thus, its order is
one. The highest
power raised to ![]() is three.
Hence, its degree
is three.
is three.
Hence, its degree
is three.
(iii) The differential equation is given as:
The highest
order derivative present
in the differential equation is ![]() . Thus, its order is four.
. Thus, its order is four.
However, the given differential equation is not a polynomial equation. Hence, its degree is not defined.
Question 2:
For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv)![]()
Answer
(i) ![]()
Differentiating both sides with respect to x, we get:
Again, differentiating both sides with respect to x, we get:
Now, on substituting the values of ![]() and
and ![]() in the differential equation,
we get:
in the differential equation,
we get:
⇒ L.H.S. ≠ R.H.S.
Hence, the given function is not a solution of the corresponding differential equation.
(ii) ![]()
Differentiating both sides with respect to x, we get:
Again, differentiating both sides with respect to x, we get:

Hence, the given function is a solution of the corresponding differential equation.
(iii) ![]()
Differentiating both sides with respect to x, we get:
Again, differentiating both sides with respect to x, we get:

![]() Substituting the value of in the L.H.S. of the given differential equation,
we get:
Substituting the value of in the L.H.S. of the given differential equation,
we get:
Hence, the given function is a solution of the corresponding differential equation.
(iv) ![]()
Differentiating both sides with respect to x, we get:
![]() Substituting the value of in the L.H.S. of the given differential equation,
we get:
Substituting the value of in the L.H.S. of the given differential equation,
we get:

Hence, the given function is a solution of the corresponding differential equation.
Question 3:
Form the differential equation representing the family of curves given by
Differentiating with respect to x, we get:
From equation (1), we get:
On substituting this value in equation (3), we get:
![]() Hence, the differential equation
of the family of curves
is given as
Hence, the differential equation
of the family of curves
is given as
Question 4:
Prove that ![]() is the general solution
of differential
is the general solution
of differential
equation
This is a homogeneous equation. To simplify it, we need to make the substitution as:
![]() Substituting the values of y and in equation (1), we get:
Substituting the values of y and in equation (1), we get:
Integrating both sides, we get:
Substituting the values of I1 and I2 in equation (3), we get:
Therefore, equation (2) becomes:

Hence, the given result is proved.
Question 5:
Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.
Answer
The equation of a circle in the first quadrant with centre (a, a) and radius (a) which touches the coordinate axes is:

Differentiating equation (1) with respect to x, we get:
Substituting the value of a in equation (1), we get:
Hence, the required differential equation of the family of circles is
Question 6:
Find the general solution of the differential equation ![]() Answer
Answer
Integrating both sides, we get:
Question 7:
Show that the general
solution of the differential equation
![]() is given by (x
+ y + 1) = A (1
– x – y – 2xy), where A
is parameter
is given by (x
+ y + 1) = A (1
– x – y – 2xy), where A
is parameter
Answer
Integrating both sides, we get:

Hence, the given result is proved.
Find the equation
of the curve passing through
the point ![]() whose differential equation is,
whose differential equation is, ![]()
Answer
The differential equation of the given curve is:
Integrating both sides, we get:
The curve passes through
point ![]()
On substituting ![]() in equation
(1), we get:
in equation
(1), we get:

![]() Hence, the required equation
of the curve is
Hence, the required equation
of the curve is
Question 9:
Find the particular solution of the differential equation
Integrating both sides, we get:
Substituting these values in equation (1), we get:
Now, y = 1 at x = 0.
Therefore, equation (2) becomes:
![]() Substituting in equation
(2), we get:
Substituting in equation
(2), we get:
This is the required particular solution of the given differential equation.
![]() Question 10:
Question 10:
Solve the differential equation
Answer
Differentiating it with respect to y, we get:
From equation (1) and equation (2), we get:
Integrating both sides, we get:

Question 11:
Find a particular solution
of the differential equation ![]() , given
that
, given
that
y = – 1, when x = 0 (Hint: put x – y = t) Answer
![]() Substituting the values of x – y and in equation (1), we get:
Substituting the values of x – y and in equation (1), we get:

Integrating both sides, we get:
Now, y = –1 at x = 0.
Therefore, equation (3) becomes:
log 1 = 0 – 1 + C
⇒ C = 1
Substituting C = 1 in equation (3) we get:
This is the required particular solution of the given differential equation.
![]() Question 12:
Question 12:
Solve the differential equation Answer

This equation is a linear differential equation of the form
The general solution of the given differential equation is given by,
Question 13:
Find a particular solution
of the differential equation ![]() ,
,
given that y = 0 when ![]() Answer
Answer
The given differential equation is:
This equation is a linear differential equation of the form

The general solution of the given differential equation is given by,
Now, ![]()
Therefore, equation (1) becomes:
![]() in equation
(1), we get:
in equation
(1), we get:
This is the required particular solution of the given differential equation.
Question 14:
Find a particular solution
of the differential equation ![]() , given
that y =
0 when x = 0
, given
that y =
0 when x = 0
Answer
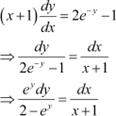
Integrating both sides, we get:
Substituting this value in equation (1), we get:
Now, at x = 0 and y = 0, equation (2) becomes:
Substituting C = 1 in equation (2), we get:

This is the required particular solution of the given differential equation.
Question 15:
The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009?
Answer
Let the population at any instant (t) be y.
It is given that the rate of increase of population is proportional to the number of inhabitants at any instant.
Integrating both sides, we get: log y = kt + C … (1)
In the year 1999, t = 0 and y = 20000. Therefore, we get:
log 20000 = C … (2)
In the year 2004, t = 5 and y = 25000. Therefore, we get:

In the year 2009, t = 10 years.
Now, on substituting the values of t, k, and C in equation (1), we get:
Hence, the population of the village in 2009 will be 31250.
Question 16:
![]() The general
solution of the differential equation is
The general
solution of the differential equation is
A. xy = C
B. x = Cy2
C. y = Cx
D. y = Cx2 Answer
The given differential equation is:
Integrating both sides, we get:
Hence, the correct answer is C.
Question 17:
The general
solution of a differential equation
of the type ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Answer
The integrating factor of the given differential equation
Hence, the correct answer is C.
Question 18:
The general solution of the differential equation ![]() is
is
A. xey + x2 = C
B. xey + y2 = C
C. yex + x2 = C
D. yey + x2 = C Answer
The given differential equation is:
This is a linear differential equation of the form
The general solution of the given differential equation is given by,
Hence, the correct answer is C.