Three Dimensional Geometry
NCERT Textbook Solution (Laptop/Desktop is best to view this page)
![]()
Exercise 11.1
Question 1:
If a line makes angles 90°, 135°, 45° with x, y and z-axes respectively, find its direction cosines.
Answer
Let direction cosines of the line be l, m, and n.
 |
Therefore, the direction cosines
of the line are ![]()
Question 2:
Find the direction cosines of a line which makes equal angles with the coordinate axes. Answer
Let the direction cosines of the line make an angle α with each of the coordinate axes.
∴ l = cos α, m = cos α, n = cos α
 |
Thus, the direction cosines of the line, which is equally inclined to the coordinate axes,
are ![]()
Question 3:
If a line has the direction ratios −18, 12, −4, then what are its direction cosines? Answer
If a line has direction ratios of −18, 12, and −4, then its direction cosines are
 |
Thus, the direction cosines
are ![]() .
.
Question 4:
Show that the points (2, 3, 4), (−1, −2, 1), (5, 8, 7) are collinear. Answer
The given points are A (2, 3, 4), B (− 1, − 2, 1), and C (5, 8, 7).
It is known that the direction ratios of line joining the points, (x1, y1, z1) and (x2, y2, z2), are given by, x2 − x1, y2 − y1, and z2 − z1.
The direction ratios of AB are (−1 − 2), (−2 − 3), and (1 − 4) i.e., −3, −5, and −3.
The direction ratios of BC are (5 − (− 1)), (8 − (− 2)), and (7 − 1) i.e., 6, 10, and 6. It can be seen that the direction ratios of BC are −2 times that of AB i.e., they are proportional.
Therefore, AB is parallel to BC. Since point B is common to both AB and BC, points A, B, and C are collinear.
 Question 5:
Question 5:
Find the direction cosines of the sides of the triangle whose vertices are (3, 5, − 4), (− 1, 1, 2) and (− 5, − 5, − 2)
Answer
The vertices of ∆ABC are A (3, 5, −4), B (−1, 1, 2), and C (−5, −5, −2).
 |
The direction ratios of side AB are (−1 − 3), (1 − 5), and (2 − (−4)) i.e., −4, −4, and 6.
 |
Therefore, the direction cosines of AB are
 |
The direction ratios of BC are (−5 − (−1)), (−5 − 1), and (−2 − 2) i.e., −4, −6, and −4. Therefore, the direction cosines of BC are

![]() The direction ratios of CA are (−5 − 3), (−5 − 5), and (−2 −
(−4)) i.e., −8,
−10, and 2. Therefore, the direction
cosines of AC are
The direction ratios of CA are (−5 − 3), (−5 − 5), and (−2 −
(−4)) i.e., −8,
−10, and 2. Therefore, the direction
cosines of AC are
 |
|||

Exercise 11.2
Question 1:
Show that the three lines with direction cosines
![]() are mutually
perpendicular.
are mutually
perpendicular.
Answer
Two lines with direction cosines, l1, m1, n1 and l2, m2, n2, are perpendicular to each other, if l1l2 + m1m2 + n1n2 = 0
(i)
For the lines with direction cosines,
![]() and
and ![]() , we obtain
, we obtain
 |
Therefore, the lines are perpendicular.
(ii)
For the lines with direction cosines,
![]() and
and ![]() , we obtain
, we obtain
 |
Therefore, the lines are perpendicular.
(iii)
![]()
![]() For the lines with direction
cosines, and , we obtain
For the lines with direction
cosines, and , we obtain

Therefore, the lines are perpendicular.
Thus, all the lines are mutually perpendicular.
Question 2:
Show that the line through the points (1, −1, 2) (3, 4, −2) is perpendicular to the line
through the points (0, 3, 2) and (3, 5, 6). Answer
Let AB be the line joining the points, (1, −1, 2) and (3, 4, − 2), and CD be the line joining the points, (0, 3, 2) and (3, 5, 6).
The direction ratios, a1, b1, c1, of AB are (3 − 1), (4 − (−1)), and (−2 − 2) i.e., 2, 5, and
−4.
The direction ratios, a2, b2, c2, of CD are (3 − 0), (5 − 3), and (6 −2) i.e., 3, 2, and 4.
AB and CD will be perpendicular to each other, if a1a2 + b1b2+ c1c2 = 0
a1a2 + b1b2+ c1c2 = 2 × 3 + 5 × 2 + (− 4) × 4
= 6 + 10 − 16
= 0
Therefore, AB and CD are perpendicular to each other.
Question 3:
Show that the line through the points (4, 7, 8) (2, 3, 4) is parallel to the line through the points (−1, −2, 1), (1, 2, 5).
Answer
Let AB be the line through the points, (4, 7, 8) and (2, 3, 4), and CD be the line through the points, (−1, −2, 1) and (1, 2, 5).
The directions ratios, a1, b1, c1, of AB are (2 − 4), (3 − 7), and (4 − 8) i.e., −2, −4, and
−4.
The direction ratios, a2, b2, c2, of CD are (1 − (−1)), (2 − (−2)), and (5 − 1) i.e., 2, 4,
and 4.
![]() AB will be parallel
to CD, if
AB will be parallel
to CD, if
 |
Thus, AB is parallel to CD.
Question 4:
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to
the vector ![]() .
.
Answer
It is given that the line passes through the point A (1, 2, 3). Therefore, the position
vector through A is ![]()
It is known that the line which passes
through point A and parallel
to ![]() is given by
is given by ![]() is a constant.
is a constant.
![]()
This is the required equation of the line.
Question 5:
Find the equation of the line in vector and in Cartesian form that passes through the
point with
position vector ![]() and is
in the direction
and is
in the direction ![]() . Answer
. Answer
It is given that the line passes through the point with position vector
![]()
![]() It is known that a line through a point with position vector
It is known that a line through a point with position vector
![]() and parallel
to
and parallel
to ![]() is given
by the equation,
is given
by the equation, ![]()
This is the required equation of the line in vector form.
Eliminating λ, we obtain the Cartesian form equation as
This is the required equation of the given line in Cartesian form.
Question 6:
Find the Cartesian equation of the line which passes through the point
(−2, 4, −5) and parallel to the line given by ![]() Answer
Answer
It is given that the line passes through the point (−2, 4, −5) and is parallel to
The direction ratios of the line, ![]() , are 3, 5, and 6. The required
line is parallel
to
, are 3, 5, and 6. The required
line is parallel
to ![]()
Therefore, its direction ratios are 3k, 5k, and 6k, where k ≠ 0
It is known that the equation of the line through the point (x1, y1, z1) and with direction
![]() ratios, a, b, c, is given by
ratios, a, b, c, is given by
Therefore the equation of the required line is
 |
Question 7:
The Cartesian equation of a line is ![]() . Write its vector form. Answer
. Write its vector form. Answer
The Cartesian equation of the line is
The given line passes through the point (5, −4, 6). The position vector of this point is
Also, the direction ratios of the given line are 3, 7, and 2.
This means that the line is in the direction of vector, ![]()
![]()
![]() It is known
that the line through position
vector and in the direction of the vector
It is known
that the line through position
vector and in the direction of the vector ![]() is given by the equation,
is given by the equation,
![]()
This is the required equation of the given line in vector form.
Question 8:
Find the vector and the Cartesian equations of the lines that pass through the origin and (5, −2, 3).
Answer
The required line passes through the origin. Therefore, its position vector is given by,
The direction ratios of the line through origin and (5, −2, 3) are (5 − 0) = 5, (−2 − 0) = −2, (3 − 0) = 3
The line is parallel
to the vector given by the equation,
![]()
The equation of the line in vector form through a point with position vector
![]() and parallel
and parallel
 to
to ![]() is,
is, ![]()
The equation of the line through the point (x1, y1, z1) and direction ratios a, b, c is given by, ![]()
Therefore, the equation of the required line in the Cartesian form is
 |
Question 9:
Find the vector and the Cartesian equations of the line that passes through the points (3,
−2, −5), (3, −2, 6).
Answer
Let the line passing through the points, P (3, −2, −5) and Q (3, −2, 6), be PQ. Since PQ passes through P (3, −2, −5), its position vector is given by,
The direction ratios of PQ are given by, (3 − 3) = 0, (−2 + 2) = 0, (6 + 5) = 11
The equation of the vector in the direction of PQ is
The equation of PQ in vector
form is given by, ![]()
The equation of PQ in Cartesian form is
![]()
![]() i.e.,
i.e.,
Question 10:
Find the angle between the following pairs of lines:
(i) ![]()
(ii) ![]() and
and
Answer
(i)  Let Q be the angle
between the given lines.
Let Q be the angle
between the given lines.
The angle between the given pairs of lines is given by,
 |
The given lines are parallel to the vectors,

(ii)
 |
The given lines are parallel to the vectors,
Question 11:
Find the angle between the following pairs of lines:
(i) ![]()
(ii) ![]()
Answer
Let ![]() and
and ![]() be the vectors parallel
to the pair of lines,
be the vectors parallel
to the pair of lines,
 |
The angle, Q, between the given pair of lines is given by the relation,
 |
(ii) Let ![]() be the vectors parallel
to the given pair of lines,
be the vectors parallel
to the given pair of lines, ![]() and
and
![]() , respectively.
, respectively.

 If Q is the angle between
the given pair of lines,
then
If Q is the angle between
the given pair of lines,
then
 |
Question 12:
Find the values of p so
the line ![]() and
and
![]() are at right angles.
are at right angles.
Answer
The given equations can be written in the standard form as

 and
and
The direction
ratios of the lines are −3, ![]() , 2 and
, 2 and ![]() respectively.
respectively.
Two lines with direction ratios, a1, b1, c1 and a2, b2, c2, are perpendicular to each other, if
a1a2 + b1 b2 + c1c2 = 0

![]() Thus, the value of p is .
Thus, the value of p is .
Question 13:
Show that the
lines ![]() and
and ![]() are
perpendicular to each other. Answer
are
perpendicular to each other. Answer
The equations of the given lines are ![]() and
and ![]()
The direction ratios of the given lines are 7, −5, 1 and 1, 2, 3 respectively.
Two lines with direction ratios, a1, b1, c1 and a2, b2, c2, are perpendicular to each other, if
a1a2 + b1 b2 + c1c2 = 0
∴ 7 × 1 + (−5) × 2 + 1 × 3
= 7 − 10 + 3
= 0
Therefore, the given lines are perpendicular to each other.
Question 14:
Find the shortest distance between the lines
 |
Answer
The equations of the given lines are
 |
 |
It is known that the shortest distance between the lines,
Comparing the given equations, we obtain
 |
Substituting all the values in equation (1), we obtain

![]() Therefore, the shortest distance
between the two lines is units.
Therefore, the shortest distance
between the two lines is units.
Question 15:
Find the shortest distance
between the lines ![]() and
and ![]() Answer
Answer
The given lines are ![]() and
and ![]() It is known that the shortest distance
between the two lines,
It is known that the shortest distance
between the two lines,
![]()
 Comparing the given equations, we obtain
Comparing the given equations, we obtain
, is given by,

 |
Substituting all the values in equation (1), we obtain
Since distance is always non-negative, the distance between
the given lines is
![]() units.
units.
Question 16:
Find the shortest distance between the lines whose vector equations are
 |
Answer
The given lines are ![]() and
and ![]()
It is known that the shortest
distance between the lines, ![]() and
and ![]() , is given by,
, is given by,

 |
Comparing the given equations with
Substituting all the values in equation (1), we obtain
Therefore, the shortest distance
between the two given lines is ![]() units.
units.
Question 17:
Find the shortest distance between the lines whose vector equations are
 |
Answer
The given lines are

 |
 |
It is known that the shortest distance between the lines,
For the given equations,
 |
Substituting all the values in equation (3), we obtain
![]() Therefore, the shortest distance
between the lines is units.
Therefore, the shortest distance
between the lines is units.
Exercise 11.3
Question 1:
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
(a)z = 2 (b) ![]()
(c) ![]() (d)5y + 8
= 0
(d)5y + 8
= 0
Answer
(a) The equation of the plane is z = 2 or 0x + 0y + z = 2 … (1) The direction ratios of normal are 0, 0, and 1.
![]() ∴
∴
Dividing both sides of equation (1) by 1, we obtain
This is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.
Therefore, the direction cosines are 0, 0, and 1 and the distance of the plane from the origin is 2 units.
(b) x + y + z = 1 … (1)
![]() The direction
ratios of normal
are 1, 1, and 1.
The direction
ratios of normal
are 1, 1, and 1.
∴
Dividing both sides of equation (1) by ![]() , we obtain
, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the
direction cosines of the normal are ![]() and the
distance of normal from the origin is
and the
distance of normal from the origin is ![]() units.
units.
(c) 2x + 3y − z = 5 … (1)
The direction ratios of normal are 2, 3, and −1.
Dividing both sides of equation (1) by ![]() , we obtain
, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the direction cosines
of the normal to the plane are ![]() and the distance of normal from the origin
is
and the distance of normal from the origin
is ![]() units.
units.
(d) 5y + 8 = 0
⇒ 0x − 5y + 0z = 8 … (1)
The direction ratios of normal are 0, −5, and 0.
Dividing both sides of equation (1) by 5, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
Therefore, the direction cosines of the normal to the plane are 0, −1, and 0 and the
distance of normal from the origin is ![]() units.
units.
Question 2:
Find the vector equation of a plane which is at a distance of 7 units from the origin and
normal to the vector ![]() . Answer
. Answer
The normal vector is, ![]()
 |
It is known that the equation
of the plane with position
vector ![]() is given
by,
is given
by, ![]()
This is the vector equation of the required plane.
Question 3:
Find the Cartesian equation of the following planes:
(a) ![]() (b)
(b) ![]()
(c) ![]()
Answer
(a) It is given that equation of the plane is
For any arbitrary point P (x, y, z) on the plane,
position vector ![]() is given by,
is given by,
Substituting the value
of ![]() in equation
(1), we obtain
in equation
(1), we obtain
This is the Cartesian equation of the plane.
(b) ![]()
For any arbitrary
point P (x, y, z) on the plane, position vector
![]() is given by,
is given by,
Substituting the value of ![]() in equation
(1), we obtain
in equation
(1), we obtain
This is the Cartesian equation of the plane.
(c) ![]()
For any arbitrary
point P (x, y, z) on the plane,
position vector ![]() is given by,
is given by,
Substituting the value
of ![]() in equation (1), we obtain
in equation (1), we obtain
 |
This is the Cartesian equation of the given plane.
Question 4:
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
Answer
(a) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x1, y1, z1).
2x + 3y + 4z − 12 = 0
⇒ 2x + 3y + 4z = 12 … (1)
The direction ratios of normal are 2, 3, and 4.
Dividing both sides of equation (1) by ![]() , we obtain
, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by (ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are
(b) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x1,
y1, z1).
⇒ ![]() … (1)
… (1)
The direction ratios of the normal are 0, 3, and 4.
Dividing both sides of equation (1) by 5, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by (ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are
(c) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x1,
y1, z1).
![]() … (1)
… (1)
The direction ratios of the normal are 1, 1, and 1.
Dividing both sides of equation (1) by ![]() , we obtain
, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by (ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are
(d) Let the coordinates of the foot of perpendicular P from the origin to the plane be (x1,
y1, z1).
⇒ 0x − 5y + 0z = 8 … (1)
The direction ratios of the normal are 0, −5, and 0.
![]()
Dividing both sides of equation (1) by 5, we obtain
This equation is of the form lx + my + nz = d, where l, m, n are the direction cosines of normal to the plane and d is the distance of normal from the origin.
The coordinates of the foot of the perpendicular are given by (ld, md, nd).
Therefore, the coordinates of the foot of the perpendicular are
Question 5:
Find the vector and Cartesian equation of the planes
(a)
that passes through the point (1, 0, −2) and the normal
to the plane is ![]() .
.
(b) that passes through the point (1, 4, 6) and the normal vector to the plane is
![]() .
.
Answer
(a) The position vector of point (1, 0, −2) is ![]()
![]() The normal vector
The normal vector ![]() perpendicular to the plane is
perpendicular to the plane is
![]() The vector
equation of the plane is given by,
The vector
equation of the plane is given by,
![]() is the position
vector of any point P (x, y, z) in the plane.
is the position
vector of any point P (x, y, z) in the plane.
Therefore, equation (1) becomes

This is the Cartesian equation of the required plane.
(b)
The position
vector of the point (1, 4, 6) is ![]() The
normal vector
The
normal vector ![]() perpendicular to the plane is
perpendicular to the plane is ![]()
The vector equation of the plane is given by,
![]() is the position
vector of any point P (x, y, z) in the plane.
is the position
vector of any point P (x, y, z) in the plane.
Therefore, equation (1) becomes
 |
This is the Cartesian equation of the required plane.
Question 6:
Find the equations of the planes that passes through three points. (a) (1, 1, −1), (6, 4, −5), (−4, −2, 3)
(b) (1, 1, 0), (1, 2, 1), (−2, 2, −1)
Answer
(a) The given points are A (1, 1, −1), B (6, 4, −5), and C (−4, −2, 3).

Since A, B, C are collinear points, there will be infinite number of planes passing through the given points.
(b) The given points are A (1, 1, 0), B (1, 2, 1), and C (−2, 2, −1).
 |
Therefore, a plane will pass through the points A, B, and C.
 It is known that the equation
of the plane through the points,
It is known that the equation
of the plane through the points, ![]()
![]() , and
, and ![]() , is
, is
This is the Cartesian equation of the required plane.
Question 7:
Find the intercepts cut off by the plane
Dividing both sides of equation (1) by 5, we obtain
 |
It is known that the equation
of a plane in intercept form is ![]() , where
a, b, c
, where
a, b, c
are the intercepts cut off by the plane at x, y, and z axes respectively. Therefore, for the given equation,
Thus, the intercepts cut off by the plane are ![]() .
.
Question 8:
Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane. Answer
The equation of the plane ZOX is
y = 0
Any plane parallel to it is of the form, y = a
Since the y-intercept of the plane is 3,
∴ a = 3
Thus, the equation of the required plane is y = 3
Question 9:
Find the equation of the plane through the intersection of the planes
![]()
![]() and and the point (2, 2, 1)
and and the point (2, 2, 1)
Answer
The equation of any plane through the intersection of the planes, 3x − y + 2z − 4 = 0 and x + y + z − 2 = 0, is
The plane passes through the point (2, 2, 1). Therefore, this point will satisfy equation (1).

 |
Substituting
This is the required equation of the plane.
Question 10:
Find the vector equation of the plane passing through the intersection of the planes
![]() and through the point
(2, 1, 3) Answer
and through the point
(2, 1, 3) Answer
![]() The equations of the planes
are
The equations of the planes
are
 |
The equation of any plane through the intersection of the planes given in equations (1) and (2) is given by,
![]() , where
, where ![]()

The plane passes through the point (2, 1, 3). Therefore, its position vector is given by,
Substituting in equation (3), we obtain
 |
Substituting ![]() in equation
(3), we obtain
in equation
(3), we obtain
 |
This is the vector equation of the required plane.
Question 11:
Find the equation of the plane through the line of intersection of the planes
![]()
![]()
![]() and which is perpendicular to the plane
and which is perpendicular to the plane
Answer
The equation of the plane through the intersection of the planes,
The direction ratios, a1, b1, c1, of this plane are (2λ
+ 1), (3λ + 1), and (4λ
+ 1). The plane in equation (1) is perpendicular to ![]()
 |
Its direction ratios, a2, b2, c2, are 1, −1, and 1. Since the planes are perpendicular,
 in equation
(1), we obtain
in equation
(1), we obtain
This is the required equation of the plane.
Question 12:
Find the angle between the planes whose vector equations are
![]()
![]() and
and
.
Answer
![]()
![]() The equations of the given planes
are and
The equations of the given planes
are and
It is known that if
![]() Here,
Here,
 |
 |
Substituting the value of
Question 13:
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
(a) ![]()
(b) ![]()
(c)![]()
(d) ![]()
(e)![]() Answer
Answer
The direction ratios of normal to the plane,
![]() , are a1, b1, c1 and
, are a1, b1, c1 and
![]() .
.
 |
The angle between L1 and L2 is given by,
 |
(a) The equations of the planes are 7x + 5y + 6z + 30 = 0 and 3x − y − 10z + 4 = 0
Here, a1 = 7, b1 =5, c1 = 6
![]()
Therefore, the given planes are not perpendicular.
![]() It can be seen that,
It can be seen that,
 |
Therefore, the given planes are not parallel. The angle between them is given by,
(b)
The equations of the planes are ![]() and
and ![]() Here,
Here, ![]() and
and ![]()
![]()
Thus, the given planes are perpendicular to each other.
(c)
The equations of the given planes are
Thus, the given planes are not perpendicular to each other.
![]() ∴
∴
Thus, the given planes are parallel to each other.
(d) ![]() The
equations of the planes are
The
equations of the planes are ![]() and
and ![]() Here,
Here,
![]() and
and
![]()
![]() ∴
∴
Thus, the given lines are parallel to each other.
(e)
The equations of the given planes are
Therefore, the given lines are not perpendicular to each other.
∴ ![]()
Therefore, the given lines are not parallel to each other. The angle between the planes is given by,
Question 14:
In the following cases, find the distance of each of the given points from the corresponding given plane.
Point Plane
(a) (0, 0, 0) ![]()
(b) (3, −2, 1) ![]()
(c) (2, 3, −5) ![]()
(d) (−6, 0, 0) ![]()
Answer
It is known that the distance between a point, p(x1, y1, z1), and a plane, Ax + By + Cz =
D, is given by,
(a)
The given point is (0, 0, 0) and the plane is ![]()
 |
(b)
 The given point is (3, − 2, 1) and the plane is
The given point is (3, − 2, 1) and the plane is ![]()
∴
(c)
The given point is (2, 3, −5) and the plane is ![]()
 |
(d)
![]() The given point is (−6, 0, 0) and the plane is
The given point is (−6, 0, 0) and the plane is

Miscellaneous Solutions
Question 1:
Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, −1), (4, 3, −1).
Answer
Let OA be the line joining the origin, O (0, 0, 0), and the point, A (2, 1, 1).
Also, let BC be the line joining the points, B (3, 5, −1) and C (4, 3, −1).
The direction ratios of OA are 2, 1, and 1 and of BC are (4 − 3) = 1, (3 − 5) = −2, and
(−1 + 1) = 0
OA is perpendicular to BC, if a1a2 + b1b2 + c1c2 = 0
∴ a1a2 + b1b2 + c1c2 = 2 × 1 + 1 (−2) + 1 ×0 = 2 − 2 = 0
Thus, OA is perpendicular to BC.
Question 2:
If l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are m1n2 − m2n1, n1l2 − n2l1, l1m2 − l2m1.
Answer
It is given that l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines. Therefore,
Let l, m, n be the direction cosines of the line which is perpendicular to the line with direction cosines l1, m1, n1 and l2, m2, n2.

l, m, n are the direction cosines of the line.
∴ l2 + m2 + n2 = 1 … (5)
It is known that,
 |
![]() ∴
∴
Substituting the values from equations (5) and (6) in equation (4), we obtain
 |
![]() Thus, the direction cosines
of the required line are
Thus, the direction cosines
of the required line are
Question 3:
Find the angle between the lines whose direction ratios are a, b, c and b − c, c − a, a − b.
Answer
 |
The angle Q between the lines with direction cosines, a, b, c and b − c, c − a, a − b, is given by,
Thus, the angle between the lines is 90°.
Question 4:
Find the equation of a line parallel to x-axis and passing through the origin. Answer
The line parallel to x-axis and passing through the origin is x-axis itself.
Let A be a point on x-axis. Therefore, the coordinates of A are given by (a, 0, 0), where
a ∈ R.
 |
Direction ratios of OA are (a − 0) = a, 0, 0 The equation of OA is given by,
Thus, the equation of line parallel to x-axis and passing through origin is
![]()
Question 5:
If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (−4, 3, −6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.
Answer
The coordinates of A, B, C, and D are (1, 2, 3), (4, 5, 7), (−4, 3, −6), and
(2, 9, 2) respectively.
The direction ratios of AB are (4 − 1) = 3, (5 − 2) = 3, and (7 − 3) = 4
The direction ratios of CD are (2 −(− 4)) = 6, (9 − 3) = 6, and (2 −(−6)) = 8
It can be seen that, ![]() Therefore, AB is parallel to CD.
Therefore, AB is parallel to CD.
Thus, the angle between AB and CD is either 0° or 180°.
sQuestion 6:
If the lines ![]() and
and ![]() are perpendicular, find the value of k.
are perpendicular, find the value of k.
Answer
The direction of
ratios of the lines, ![]() and
and ![]() , are
−3, 2k, 2 and 3k, 1, −5 respectively.
, are
−3, 2k, 2 and 3k, 1, −5 respectively.
 |
It is known that two lines with direction ratios, a1, b1, c1 and a2, b2, c2, are perpendicular, if a1a2 + b1b2 + c1c2 = 0
Therefore, for ![]() , the given lines are perpendicular to each other.
, the given lines are perpendicular to each other.
Question 7:
Find the vector equation of the plane passing through (1, 2, 3) and perpendicular to the
plane ![]() Answer
Answer
The position vector of the point (1, 2, 3) is ![]()
The direction
ratios of the normal to the plane, ![]() ,
are 1, 2, and −5 and the normal vector
is
,
are 1, 2, and −5 and the normal vector
is ![]()
The equation of a line passing through a point and perpendicular to the given plane is
given by,
Question 8:
Find the equation of the plane passing through (a, b, c) and parallel to the plane
Answer
![]() Any plane parallel to the plane,
Any plane parallel to the plane,
![]() , is of the form
, is of the form
The plane passes through
the point (a, b, c). Therefore, the position vector ![]() of this point is
of this point is ![]()
Therefore, equation (1) becomes
![]() Substituting
Substituting ![]() in equation
(1), we obtain
in equation
(1), we obtain
This is the
vector equation of the required plane. Substituting ![]() in equation
(2), we obtain
in equation
(2), we obtain
Question 9:
Find the shortest distance
between lines ![]() and
and ![]() .
.
Answer
The given lines are
 |
 |
It is known that the shortest distance between two lines,
![]() Comparing to equations (1) and (2), we obtain
Comparing to equations (1) and (2), we obtain
 |
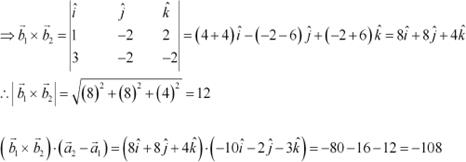
Substituting all the values in equation (1), we obtain
Therefore, the shortest distance between the two given lines is 9 units.
Question 10:
Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the YZ-plane
Answer
It is known that the equation of the line passing through the points, (x1, y1, z1) and (x2,
![]() y2, z2), is
y2, z2), is
The line passing through the points, (5, 1, 6) and (3, 4, 1), is given by,
 |
Any point on the line is of the form (5 − 2k, 3k + 1, 6 −5k). The equation of YZ-plane is x = 0
Since the line passes through YZ-plane, 5 − 2k = 0

![]() Therefore, the required point is .
Therefore, the required point is .
Question 11:
Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX − plane.
Answer
It is known that the equation of the line passing through the points, (x1, y1, z1) and (x2,
![]() y2, z2), is
y2, z2), is
The line passing through the points, (5, 1, 6) and (3, 4, 1), is given by,
 |
Any point on the line is of the form (5 − 2k, 3k + 1, 6 −5k). Since the line passes through ZX-plane,

 |
![]() Therefore, the required point is .
Therefore, the required point is .
Question 12:
Find the coordinates of the point where the line through (3, −4, −5) and (2, − 3, 1) crosses the plane 2x + y + z = 7).
Answer
It is known that the equation of the line through the points, (x1, y1, z1) and (x2, y2, z2), is
Since the line passes through the points, (3, −4, −5) and (2, −3, 1), its equation is given by,

Therefore, any point on the line is of the form (3 − k, k − 4, 6k − 5). This point lies on the plane, 2x + y + z = 7
∴ 2 (3 − k) + (k − 4) + (6k − 5) = 7
Hence, the coordinates of the required point are (3 − 2, 2 − 4, 6 × 2 − 5) i.e.,
(1, −2, 7).
Question 13:
Find the equation of the plane passing through the point (−1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
Answer
The equation of the plane passing through the point (−1, 3, 2) is
a (x + 1) + b (y − 3) + c (z − 2) = 0 … (1)
where, a, b, c are the direction ratios of normal to the plane.
It is known that two planes,
![]() and
and ![]() , are
, are
perpendicular, if ![]()
Plane (1) is perpendicular to the plane, x + 2y + 3z = 5
Also, plane (1) is perpendicular to the plane, 3x + 3y + z = 0
From equations (2) and (3), we obtain
 |
Substituting the values of a, b, and c in equation (1), we obtain
 |
This is the required equation of the plane.
Question 14:
If the points (1, 1, p) and (−3, 0, 1) be equidistant from the plane
![]() , then find the value
of p. Answer
, then find the value
of p. Answer
The position vector through the point (1, 1, p) is
The equation of the given plane
is ![]()
It is known that the perpendicular distance between a point whose position vector is

![]() and the plane,
and the plane, ![]() is given
by,
is given
by,
![]() Here,
Here, ![]() and d
and d
Therefore, the distance between the point (1, 1, p) and the given plane is
Similarly, the distance between the point (−3, 0, 1) and the given plane is
It is given that the distance between the required plane and the points, (1, 1, p) and (−3, 0, 1), is equal.
∴ D1 = D2

Question 15:
Find the equation of the plane passing through the line of intersection of the planes
![]() and
and ![]() and
parallel to x-axis. Answer
and
parallel to x-axis. Answer
The given planes are
The equation of any plane passing through the line of intersection of these planes is
Its direction ratios are (2λ + 1), (3λ + 1), and (1 − λ).
The required plane is parallel to x-axis. Therefore, its normal is perpendicular to x-axis. The direction ratios of x-axis are 1, 0, and 0.
![]() Substituting in equation
(1), we obtain
Substituting in equation
(1), we obtain
Therefore, its Cartesian equation is y − 3z + 6 = 0 This is the equation of the required plane.
Question 16:
If O be the origin and the coordinates of P be (1, 2, −3), then find the equation of the plane passing through P and perpendicular to OP.
Answer
The coordinates of the points, O and P, are (0, 0, 0) and (1, 2, −3) respectively.
Therefore, the direction ratios of OP are (1 − 0) = 1, (2 − 0) = 2, and (−3 − 0) = −3 It is known that the equation of the plane passing through the point (x1, y1 z1) is
![]() where, a, b, and c are
the direction ratios
of normal. Here,
the direction ratios
of normal are 1, 2, and −3
and the point P is (1, 2, −3).
where, a, b, and c are
the direction ratios
of normal. Here,
the direction ratios
of normal are 1, 2, and −3
and the point P is (1, 2, −3).
Thus, the equation of the required plane is
Question 17:
Find the equation of the plane which contains the line of intersection of the planes
![]()
![]() , and which
is perpendicular to the plane
, and which
is perpendicular to the plane
![]() .
.
Answer
The equations of the given planes are
The equation of the plane passing through the line intersection of the plane given in equation (1) and equation (2) is

The plane in equation (3) is perpendicular to the plane,
This is the vector equation of the required plane.
The Cartesian equation of this plane can be obtained by substituting
Question 18:
Find the distance of the point (−1, −5, −10) from the point of intersection of the line
![]()
![]() and the plane
and the plane
.
Answer
The equation of the given line is
The equation of the given plane is
Substituting the value of ![]() from equation
(1) in equation (2), we obtain
from equation
(1) in equation (2), we obtain

Substituting this value in equation (1), we obtain the equation of the line as
![]() This means
that the position
vector of the point of intersection of the line and the plane is
This means
that the position
vector of the point of intersection of the line and the plane is ![]()
This shows that the point of intersection of the given line and plane is given by the coordinates, (2, −1, 2). The point is (−1, −5, −10).
The distance d between the points, (2, −1, 2) and (−1, −5, −10), is
Question 19:
Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes
![]() and
and ![]() Answer
Answer
Let the required
line be parallel to vector
![]() given by,
given by,
The position vector of the point (1, 2, 3) is ![]()
The equation of line passing through
(1, 2, 3) and parallel
to ![]() is given
by,
is given
by,
The equations of the given planes are

The line in equation (1) and plane in equation (2) are parallel. Therefore, the normal to the plane of equation (2) and the given line are perpendicular.
From equations (4) and (5), we obtain
Therefore, the direction ratios
of ![]() are −3,
5, and 4.
are −3,
5, and 4.
Substituting the value of ![]() in equation
(1), we obtain
in equation
(1), we obtain
This is the equation of the required line.
Question 20:
Find the vector equation of the line passing through the point (1, 2, − 4) and
perpendicular to the two lines:
![]() Answer
Answer
![]() Let the required
line be parallel to the vector
Let the required
line be parallel to the vector ![]() given by,
given by,
![]() The position
vector of the point (1, 2, −
4) is
The position
vector of the point (1, 2, −
4) is
The equation of the line passing
through (1, 2, −4) and parallel to vector ![]() is
is
The equations of the lines are
Line (1) and line (2) are perpendicular to each other.
Also, line (1) and line (3) are perpendicular to each other.
From equations (4) and (5), we obtain
∴Direction ratios
of ![]() are 2, 3, and 6.
are 2, 3, and 6.
Substituting ![]() in equation
(1), we obtain
in equation
(1), we obtain
This is the equation of the required line.
Question 21:
Prove that if a plane has the intercepts a, b, c and is at a distance of P units from the
![]() origin, then Answer
origin, then Answer
The equation of a plane having intercepts a, b, c with x, y, and z axes respectively is given by,
The distance (p) of the plane from the origin is given by,
Question 22:
Distance between
the two planes: ![]() and
and ![]() is (A)2 units (B)4 units (C)8 units
is (A)2 units (B)4 units (C)8 units
(D) ![]()
Answer
The equations of the planes are
![]()
It can be seen that the given planes are parallel.
It is known that the distance between two parallel planes, ax + by + cz = d1 and ax + by
+ cz = d2, is given by,
Thus, the distance between the lines is ![]() units. Hence,
the correct answer
is D.
units. Hence,
the correct answer
is D.
Question 23:
The planes: 2x − y + 4z = 5 and 5x − 2.5y + 10z = 6 are
(A) Perpendicular (B) Parallel (C) intersect y-axis
(C) passes
through ![]() Answer
Answer
The equations of the planes are 2x − y + 4z = 5 … (1)
5x − 2.5y + 10z = 6 … (2)
It can be seen that,
![]()
![]()

![]() ∴
∴
Therefore, the given planes are parallel. Hence, the correct answer is B.