Atoms
NCERT Textbook Solution (Laptop/Desktop is best to view this page)
Question 12.1:
Choose the correct alternative from the clues given at the end of the each statement:
The size of the atom in Thomsonís model is.......... the atomic size in Rutherfordís model.
(much greater than/no different from/much less than.)
In the ground state of .......... electrons are in stable equilibrium, while in.......... electrons
always experience a net force.
(Thomsonís model/ Rutherfordís model.)
A classical atom based on.......... is doomed to collapse.
(Thomsonís model/ Rutherfordís model.)
An atom has a nearly continuous mass distribution in a.......... but has a highly non-
uniform mass distribution in ..........
(Thomsonís model/ Rutherfordís model.)
The positively charged part of the atom possesses most of the mass in ..........
(Rutherfordís model/both the models.)
Answer
The sizes of the atoms taken in Thomsonís model and Rutherfordís model have the same order of magnitude.
In the ground state of Thomsonís model, the electrons are in stable equilibrium. However, in Rutherfordís model, the electrons always experience a net force.
A classical atom based on Rutherfordís model is doomed to collapse.
An atom has a nearly continuous mass distribution in Thomsonís model, but has a highly non-uniform mass distribution in Rutherfordís model.
The positively charged part of the atom possesses most of the mass in both the models.
![]()
Question 12.2:
Suppose you are given a chance to repeat the alpha-particle scattering experiment using a thin sheet of solid hydrogen in place of the gold foil. (Hydrogen is a solid at temperatures below 14 K.) What results do you expect?
Answer
In the alpha-particle scattering experiment, if a thin sheet of solid hydrogen is used in place of a gold foil, then the scattering angle would not be large enough. This is because the mass of hydrogen (1.67 ◊ 10−27 kg) is less than the mass of incident α−particles (6.64
◊ 10−27 kg). Thus, the mass of the scattering particle is more than the target nucleus (hydrogen). As a result, the α−particles would not bounce back if solid hydrogen is used in the α-particle scattering experiment.
![]()
Question 12.3:
What is the shortest wavelength present in the Paschen series of spectral lines?
Answer
Rydbergís formula is given as:
Where,
h = Planckís constant = 6.6 ◊ 10−34 Js
c = Speed of light = 3 ◊ 108 m/s
(n1 and n2 are integers)
The shortest wavelength present in the Paschen series of the spectral lines is given for values n1 = 3 and n2 = ∞.
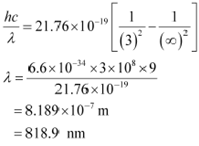
![]()
Question 12.4:
A difference of 2.3 eV separates two energy levels in an atom. What is the frequency of radiation emitted when the atom makes a transition from the upper level to the lower level?
Answer
Separation of two energy levels in an atom,
E = 2.3 eV
= 2.3 ◊ 1.6 ◊ 10−19
= 3.68 ◊ 10−19 J
Let ν be the frequency of radiation emitted when the atom transits from the upper level to
the lower level.
We have the relation for energy as:
E = hv
Where,
h = Planckís constant
![]()
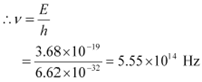 |
Hence, the frequency of the radiation is 5.6 ◊ 1014 Hz.
![]()
Question 12.5:
The ground state energy of hydrogen atom is −13.6 eV. What are the kinetic and potential
energies of the electron in this state?
Answer
Ground state energy of hydrogen atom, E = − 13.6 eV
This is the total energy of a hydrogen atom. Kinetic energy is equal to the negative of the total energy.
Kinetic energy = − E = − (− 13.6) = 13.6 eV
Potential energy is equal to the negative of two times of kinetic energy.
Potential energy = − 2 ◊ (13.6) = − 27 .2 eV
![]()
Question 12.6:
A hydrogen atom initially in the ground level absorbs a photon, which excites it to the n = 4 level. Determine the wavelength and frequency of the photon.
Answer
For ground level, n1 = 1
Let E1 be the energy of this level. It is known that E1 is related with n1 as:
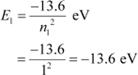
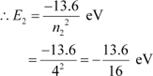 |
The atom is excited to a higher level, n2 = 4. Let E2 be the energy of this level.
The amount of energy absorbed by the photon is given as:
E = E2 − E1
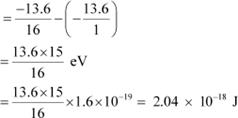 |
For a photon of wavelengthλ, the expression of energy is written as:
Where,
h = Planckís constant = 6.6 ◊ 10−34 Js
c = Speed of light = 3 ◊ 108 m/s
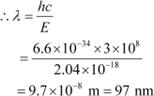 |
And, frequency of a photon is given by the relation,
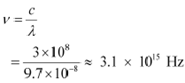
Hence, the wavelength of the photon is 97 nm while the frequency is 3.1 ◊ 1015 Hz.
![]()
Question 12.7:
Using the Bohrís model calculate the speed of the electron in a hydrogen atom in the n = 1, 2, and 3 levels. (b) Calculate the orbital period in each of these levels.
Answer
Let ν1 be the orbital speed of the electron in a hydrogen atom in the ground state level, n1
= 1. For charge (e) of an electron, ν1 is given by the relation,
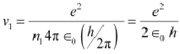 |
Where,
e = 1.6 ◊ 10−19 C
∈0 = Permittivity of free space = 8.85 ◊ 10−12 N−1 C2 m−2
h = Planckís constant = 6.62 ◊ 10−34 Js
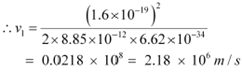 |
For level n2 = 2, we can write the relation for the corresponding orbital speed as:
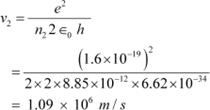
And, for n3 = 3, we can write the relation for the corresponding orbital speed as:
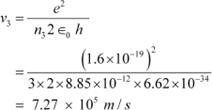 |
Hence, the speed of the electron in a hydrogen atom in n = 1, n=2, and n=3 is 2.18 ◊ 106 m/s, 1.09 ◊ 106 m/s, 7.27 ◊ 105 m/s respectively.
Let T1 be the orbital period of the electron when it is in level n1 = 1. Orbital period is related to orbital speed as:
Where,
r1 = Radius of the orbit
h = Planckís constant = 6.62 ◊ 10−34 Js
e = Charge on an electron = 1.6 ◊ 10−19 C
∈0 = Permittivity of free space = 8.85 ◊ 10−12 N−1 C2 m−2
m = Mass of an electron = 9.1 ◊ 10−31 kg
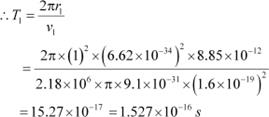
For level n2 = 2, we can write the period as:
Where,
r2 = Radius of the electron in n2 = 2
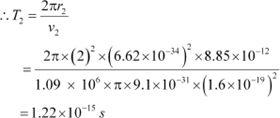 |
And, for level n3 = 3, we can write the period as:
Where,
r3 = Radius of the electron in n3 = 3
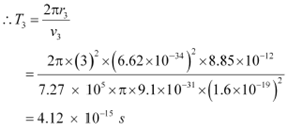
Hence, the orbital period in each of these levels is 1.52 ◊ 10−16 s, 1.22 ◊ 10−15 s, and 4.12
◊ 10−15 s respectively.
![]()
Question 12.8:
The radius of the innermost electron orbit of a hydrogen atom is 5.3 ◊10−11 m. What are the radii of the n = 2 and n =3 orbits?
Answer
The radius of the innermost orbit of a hydrogen atom, r1 = 5.3 ◊ 10−11 m.
Let r2 be the radius of the orbit at n = 2. It is related to the radius of the innermost orbit as:
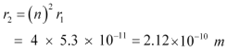 |
For n = 3, we can write the corresponding electron radius as:
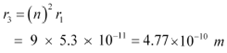 |
Hence, the radii of an electron for n = 2 and n = 3 orbits are 2.12 ◊ 10−10 m and 4.77 ◊ 10−10 m respectively.
![]()
Question 12.9:
A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. What series of wavelengths will be emitted?
Answer
It is given that the energy of the electron beam used to bombard gaseous hydrogen at room temperature is 12.5 eV. Also, the energy of the gaseous hydrogen in its ground state at room temperature is −13.6 eV.
When gaseous hydrogen is bombarded with an electron beam, the energy of the gaseous hydrogen becomes −13.6 + 12.5 eV i.e., −1.1 eV.
Orbital energy is related to orbit level (n) as:
![]() For n = 3,
For n = 3,
This energy is approximately equal to the energy of gaseous hydrogen. It can be concluded that the electron has jumped from n = 1 to n = 3 level.
During its de-excitation, the electrons can jump from n = 3 to n = 1 directly, which forms a line of the Lyman series of the hydrogen spectrum.
We have the relation for wave number for Lyman series as:
Where,
Ry = Rydberg constant = 1.097 ◊ 107 m−1
λ= Wavelength of radiation emitted by the transition of the electron For n = 3, we can obtain λas:
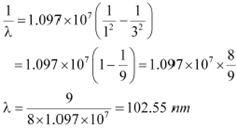
If the electron jumps from n = 2 to n = 1, then the wavelength of the radiation is given as:
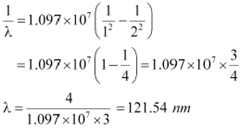 |
If the transition takes place from n = 3 to n = 2, then the wavelength of the radiation is given as:
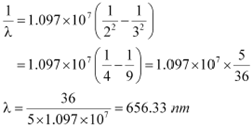 |
This radiation corresponds to the Balmer series of the hydrogen spectrum.
Hence, in Lyman series, two wavelengths i.e., 102.5 nm and 121.5 nm are emitted. And in the Balmer series, one wavelength i.e., 656.33 nm is emitted.
![]()
Question 12.10:
In accordance with the Bohrís model, find the quantum number that characterises the earthís revolution around the sun in an orbit of radius 1.5 ◊ 1011 m with orbital speed 3 ◊ 104 m/s. (Mass of earth = 6.0 ◊ 1024 kg.)
Answer
Radius of the orbit of the Earth around the Sun, r = 1.5 ◊ 1011 m Orbital speed of the Earth, ν = 3 ◊ 104 m/s
Mass of the Earth, m = 6.0 ◊ 1024 kg
According to Bohrís model, angular momentum is quantized and given as:
Where,
h = Planckís constant = 6.62 ◊ 10−34 Js
n = Quantum number
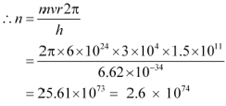 |
Hence, the quanta number that characterizes the Earthí revolution is 2.6 ◊ 1074.
![]()
Question 12.11:
Answer the following questions, which help you understand the difference between Thomsonís model and Rutherfordís model better.
Is the average angle of deflection of α-particles by a thin gold foil predicted by Thomsonís model much less, about the same, or much greater than that predicted by Rutherfordís model?
Is the probability of backward scattering (i.e., scattering of α-particles at angles greater than 90į) predicted by Thomsonís model much less, about the same, or much greater than that predicted by Rutherfordís model?
Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α-particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide?
In which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scattering of α-particles by a thin foil?
Answer
about the same
The average angle of deflection of α-particles by a thin gold foil predicted by Thomsonís model is about the same size as predicted by Rutherfordís model. This is because the average angle was taken in both models.
much less
The probability of scattering of α-particles at angles greater than 90į predicted by Thomsonís model is much less than that predicted by Rutherfordís model.
Scattering is mainly due to single collisions. The chances of a single collision increases linearly with the number of target atoms. Since the number of target atoms increase with an increase in thickness, the collision probability depends linearly on the thickness of the target.
Thomsonís model
It is wrong to ignore multiple scattering in Thomsonís model for the calculation of average angle of scattering of α−particles by a thin foil. This is because a single collision causes very little deflection in this model. Hence, the observed average scattering angle can be explained only by considering multiple scattering.
![]()
Question 12.12:
The gravitational attraction between electron and proton in a hydrogen atom is weaker than the coulomb attraction by a factor of about 10−40. An alternative way of looking at this fact is to estimate the radius of the first Bohr orbit of a hydrogen atom if the electron and proton were bound by gravitational attraction. You will find the answer interesting.
Answer
Radius of the first Bohr orbit is given by the relation,

Where,
∈0 = Permittivity of free space
h = Planckís constant = 6.63 ◊ 10−34 Js me = Mass of an electron = 9.1 ◊ 10−31 kg e = Charge of an electron = 1.9 ◊ 10−19 C mp = Mass of a proton = 1.67 ◊ 10−27 kg
r = Distance between the electron and the proton
Coulomb attraction between an electron and a proton is given as:
Gravitational force of attraction between an electron and a proton is given as:
Where,
G = Gravitational constant = 6.67 ◊ 10−11 N m2/kg2
If the electrostatic (Coulomb) force and the gravitational force between an electron and a proton are equal, then we can write:
∴FG = FC
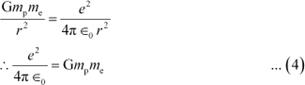 |
Putting the value of equation (4) in equation (1), we get:
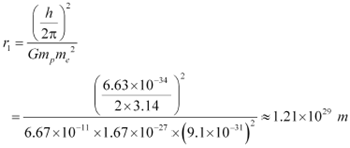
It is known that the universe is 156 billion light years wide or 1.5 ◊ 1027 m wide. Hence, we can conclude that the radius of the first Bohr orbit is much greater than the estimated size of the whole universe.
![]()
Question 12.13:
Obtain an expression for the frequency of radiation emitted when a hydrogen atom de- excites from level n to level (n−1). For large n, show that this frequency equals the classical frequency of revolution of the electron in the orbit.
Answer
It is given that a hydrogen atom de-excites from an upper level (n) to a lower level (n−1).
We have the relation for energy (E1) of radiation at level n as:
 |
 |
Now, the relation for energy (E2) of radiation at level (n − 1) is givenas:
Energy (E) released as a result of de-excitation:
E = E2−E1
hν = E2 − E1 Ö (iii) Where,
ν = Frequency of radiation emitted
Putting values from equations (i) and (ii) in equation (iii), we get:
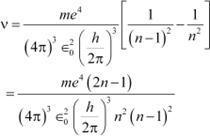 |
![]() For large n, we
can write
For large n, we
can write
 |
Classical relation of frequency of revolution of an electron is given as:
Where,
 Velocity of the electron
in the nth orbit is given as:
Velocity of the electron
in the nth orbit is given as:
v =
And, radius of the nth orbit is given as:
r = 
Putting the values of equations (vi) and (vii) in equation (v), we get:
 |
Hence, the frequency of radiation emitted by the hydrogen atom is equal to its classical orbital frequency.
![]()
Question 12.14:
Classically, an electron can be in any orbit around the nucleus of an atom. Then what determines the typical atomic size? Why is an atom not, say, thousand times bigger than its typical size? The question had greatly puzzled Bohr before he arrived at his famous model of the atom that you have learnt in the text. To simulate what he might well have done before his discovery, let us play as follows with the basic constants of nature and see if we can get a quantity with the dimensions of length that is roughly equal to the known size of an atom (~ 10−10 m).
Construct a quantity with the dimensions of length from the fundamental constants e, me, and c. Determine its numerical value.
You will find that the length obtained in (a) is many orders of magnitude smaller than the atomic dimensions. Further, it involves c. But energies of atoms are mostly in non- relativistic domain where c is not expected to play any role. This is what may have suggested Bohr to discard c and look for Ďsomething elseí to get the right atomic size.
Now, the Planckís constant h had already made its appearance elsewhere. Bohrís great insight lay in recognising that h, me, and e will yield the right atomic size. Construct a quantity with the dimension of length from h, me, and e and confirm that its numerical value has indeed the correct order of magnitude.
Answer
Charge on an electron, e = 1.6 ◊ 10−19 C
![]() Mass of an electron,
me = 9.1 ◊ 10−31 kg Speed of light, c = 3 ◊108 m/s
Mass of an electron,
me = 9.1 ◊ 10−31 kg Speed of light, c = 3 ◊108 m/s
Let us take a quantity involving the given quantities as Where,
![]() ∈0
= Permittivity of free space
∈0
= Permittivity of free space
And,
The numerical value of the taken quantity will be:
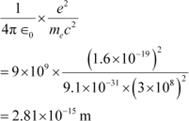 |
Hence, the numerical value of the taken quantity is much smaller than the typical size of an atom.
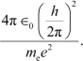 Charge on an
electron, e = 1.6 ◊ 10−19 C Mass of an electron, me = 9.1 ◊ 10−31 kg Planckís constant,
h = 6.63 ◊10−34 Js
Charge on an
electron, e = 1.6 ◊ 10−19 C Mass of an electron, me = 9.1 ◊ 10−31 kg Planckís constant,
h = 6.63 ◊10−34 Js
Let us take a quantity involving the given quantities as Where,
![]() ∈0
= Permittivity of free space
∈0
= Permittivity of free space
And,
The numerical value of the taken quantity will be:
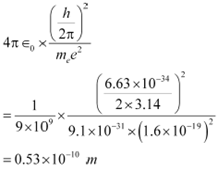
Hence, the value of the quantity taken is of the order of the atomic size.
![]()
Question 12.15:
The total energy of an electron in the first excited state of the hydrogen atom is about
−3.4 eV.
What is the kinetic energy of the electron in this state?
What is the potential energy of the electron in this state?
Which of the answers above would change if the choice of the zero of potential energy is changed?
Answer
Total energy of the electron, E = −3.4 eV
Kinetic energy of the electron is equal to the negative of the total energy.
![]() K = −E
K = −E
= − (− 3.4) = +3.4 eV
Hence, the kinetic energy of the electron in the given state is +3.4 eV.
Potential energy (U) of the electron is equal to the negative of twice of its kinetic energy.
![]() U = −2 K
U = −2 K
= − 2 ◊ 3.4 = − 6.8 eV
Hence, the potential energy of the electron in the given state is − 6.8 eV.
The potential energy of a system depends on the reference point taken. Here, the potential energy of the reference point is taken as zero. If the reference point is changed, then the value of the potential energy of the system also changes. Since total energy is the sum of kinetic and potential energies, total energy of the system will also change.
![]()
Question 12.16:
If Bohrís quantisation postulate (angular momentum = nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantisation of orbits of planets around the sun?
Answer
We never speak of quantization of orbits of planets around the Sun because the angular momentum associated with planetary motion is largely relative to the value of Planckís constant (h). The angular momentum of the Earth in its orbit is of the order of 1070h. This leads to a very high value of quantum levels n of the order of 1070. For large values of n, successive energies and angular momenta are relatively very small. Hence, the quantum levels for planetary motion are considered continuous.
![]()
Question 12.17:
Obtain the first Bohrís radius and the ground state energy of a muonic hydrogen atom [i.e., an atom in which a negatively charged muon (μ−) of mass about 207me orbits around a proton].
Answer
![]() Mass of a negatively charged muon,
Mass of a negatively charged muon,
According to Bohrís model,
![]() Bohr radius,
Bohr radius,
![]() And, energy of a ground state electronic hydrogen
atom,
And, energy of a ground state electronic hydrogen
atom,
![]() We have the value of the first Bohr orbit,
We have the value of the first Bohr orbit,
Let rμ be the radius of muonic hydrogen atom.
At equilibrium, we can write the relation as:
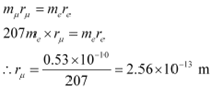 |
Hence, the value of the first Bohr radius of a muonic hydrogen atom is 2.56 ◊ 10−13 m.
We have,
Ee= − 13.6 eV
Take the ratio of these energies as:
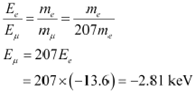 |
Hence, the ground state energy of a muonic hydrogen atom is −2.81 keV.
![]()